2020-08-09 21:41:16
关于分贝dB(decibel,[ˈdesɪbel] ),第一感觉认为是声音的大小单位,dB除了用在声学领域之外,还用在:
电子、电气、通信、音频、设计、振动等领域内,常令刚接触dB的人感到困惑的是,dB到底是什么?个人是音频小白,从自己的角度来总结一下dB的一些性质:
一、dB的常见用途有二:(1):表示声音大小;(2):表示比值大小;具体如下:
(1)表示声音大小:
在声学领域,dB经常用作为表征声压级SPL(Sound Pressure Level)的大小。声压的单位是帕斯卡,Pa,声压的参考值是20μPa,这个值表示人耳在1000Hz处的平均可听阈值,或者是人耳在1000Hz处可被感知的平均最小声压波动值。
声音是叠加在大气压之上的声压波动,大气压为1.01325×10^5Pa。相比于大气压,声压幅值波动非常小。人耳可听的声压幅值波动范围为2×10^-5Pa~20Pa,这个声压幅值波动区间很大,二者的比值达到了10^6。似乎从线性角度来说这个声压幅值的波动区间,很不方便。
数字位数一多,读起来都头痛,要仔细逐一数一数位数,我反正是这样的,我不知道您是不是也是这样!有没有懒人方法呢,能方便的反映出这个波动的幅值呢?大师Bell早就在思考:有没有好的方法解决这个问题。因此,引入了以dB表示的声压级的概念。
他发现我们人类耳朵对声音强度的反应是成对数形式的,大概意思就是当声音的强度增加到某一程度时,人的听觉会变的较不敏锐,刚好近似对数的单位刻度。这使得对数的单位可以拿来代表人类听觉变化的比例,因此,以对数dB形式表示的声压级应孕而生了。
人耳可听的声压幅值波动范围为2×10^-5Pa~20Pa,用幅值dB表示对应的分贝数为0~120dB,因此,当用分贝表示声压级的大小时,表征起来更为方便。现实世界中各种常见情况中声音分贝大小如下图所示。
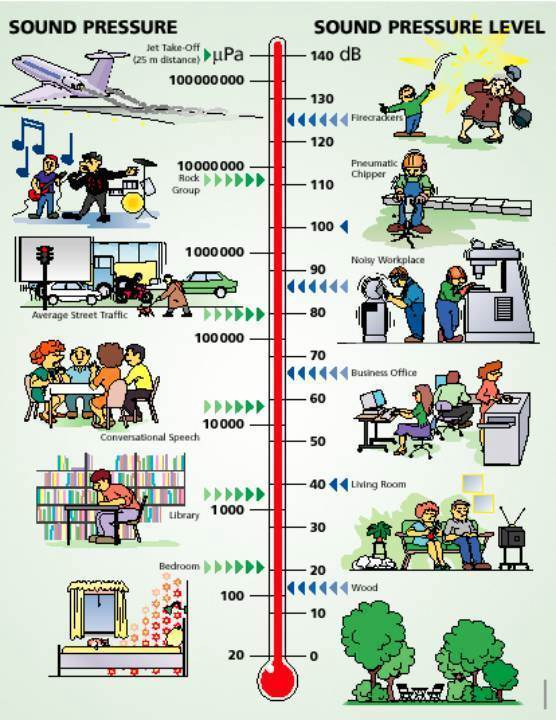
用图表表示声压幅值和分贝数如下表所示:
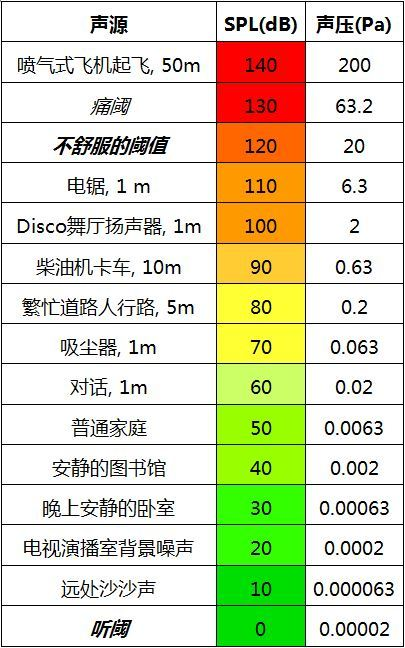
(2)表示比值大小:
dB表示放大倍数:既然有日常常用的放大2倍,放大10倍,放大100倍等等,为什么还需要dB来表示放大倍数?这是因为很多工程领域中的放大倍数的放大倍数值非常大(千万、亿级等),当用对数dB表达增益随频率变化的曲线时,可大大扩大线性增益变化的区间,就要用10的对数来表示放大倍数,这个放大倍数的单位刚好就是dB:表示放大了10的多少次方倍:
公式为:
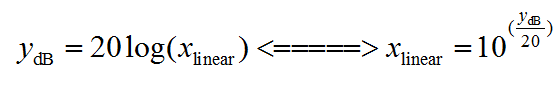
放大倍数(dB) = 20log10(x) ,其中x为线形域(也就是常说的多少倍)
例如:1、电压或电流的幅值放大1000倍即为 20*log10(1000) = 20*3 = 60dB,即表示电压放大1000倍 等价于 电压放大了60dB;
2、功率放大1000倍即为 10*log10(1000) = 10*3 = 30dB,即表示功率放大1000倍 等价于 功率放大了30dB;
使用dB的优点有如下:
(1) 当用对数dB表达增益随频率变化的曲线时,可大大扩大线性增益变化的区间。通过上一小节,我们已经明白人耳可听的声压幅值波动范围为2×10^-5Pa~20Pa,而用幅值dB表示时对应的dB数值仅仅为0~120dB。
(2) 计算多级放大的总增益时,可将乘法化为加法进行运算。
(3) dB值可正可负。正值表示增大,负值表示衰减。若x/x0<1,则dB值为负值。也就是说测量值大于参考值的为正,小于参考值的为负。
(4) 幅值比互为倒数时,dB值互为正负。
这是因为:

dB值与线性幅值比的关系如下表所示: (常见的用红色标注)
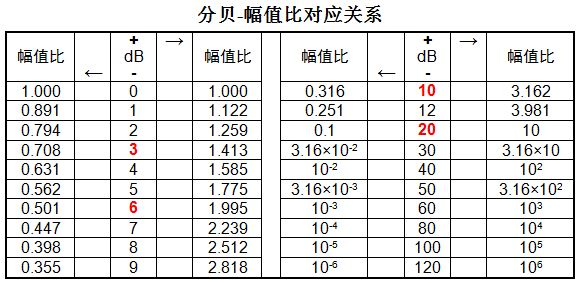
总结与拓展:
看到这里,大概知道dB的两个主要用途;其实,dB表示声压级的时候,也是声压和参考声压比值在对数域上的比值,而dB的用途远不止体现在和参考声压的比值上,相同的道理可以放在其他领域,因其无量纲的特点,可以方便地扩展到其他变量的比值上。
更多拓展链接:
两台声强 90 分贝的钢琴同时弹奏的声强是否为 180 分贝?
参考:
1. 什么是分贝dB?