芝麻OI比赛T7edges题解
题目大意
有 (n) 个点和 (m) 条无向边,木木喜欢把那些编号连续的边拿来组成一张无向图。于是,木木得到了 (frac{m(m+1)}{2}) 张无向图 (分别为编号从 (1) 到 (1),编号从 (1) 到 (2),编号从 (1) 到 (3),…,编号从 (1) 到 (n),编号从 (2) 到 (2),编号从 (2) 到 (3),…,编号从 (2) 到 (n),…,编号从 (n) 到 (n) 这些边组成的无向图)。
在一张无向图中,如果删掉一条边,这张图的连通性不变 (即原来连通的点仍然连通,原来不连通的点仍然不连通),则称这条边是多余的。
现在木木想知道,对于每一条边,它在多少张无向图中是多余的。
解题思路
由题意可知,无向图是由一段([l,r](lleq r))的边构成的,我们就可以枚举(l),然后不断的扩展(r),将边加入无向图,并统计答案,直至(r=n)。
将一条边加入无向图有两种情况:
①不与无向图原有的边构成环。那么这时候我们只用把这条边加入无向图并更新原有的数组就可以了。
②与无向图中的边构成环,这时候我们就要更新答案。
我们用(r[i])表示距离第(i)条边最近的能与其构成环的边的序号,易知第(i)条边对答案的贡献是(m-r[i]+1)
即
接下来,就是讨论如何更新了。
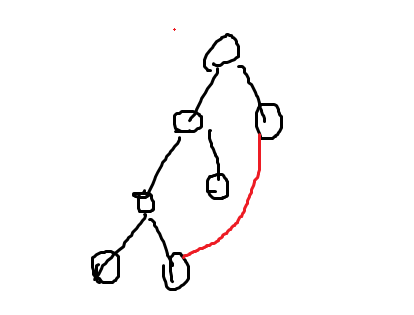
假设我们现在要添加这条红色的边。
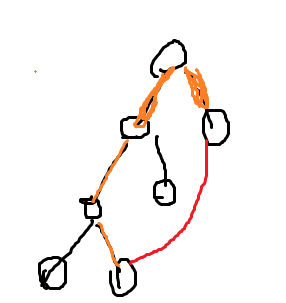
那么橙色的边上的(r[i])都是要更新的,因为它们上面的(r[i])都没有更新过。至于为什么这样,之后就会明白了。
然后,我们就要更新红色的边连接的两点在树上的路径的答案。
不难发现两个节点跳到LCA的过程就是两点在树上的路径。
于是,我们就可以边跳LCA边更新答案。
至此,更新的问题已经被我们解决了。但是这个方法只在树上有效。
不难想到把环缩成一个个点,点的编号就是环的代表节点的编号。
这样一来,每次加边操作结束后,该无向图仍然是一棵树,符合了我们的条件。
代码
被我加了注释的std
#include<bits/stdc++.h>
using namespace std;
int n,m;
int x[5005],y[5005],ans[5005];
int fa[2005],siz[2005],dep[2005],father[2005],root[2005],v[2005],r[5005];
int head[2005],Next[10005],to[10005],val[10005],tot;
void addedge(int x,int y,int z){
Next[++tot]=head[x];to[tot]=y;val[tot]=z;head[x]=tot;
}
int get(int x){
if(x==fa[x])return x;
return fa[x]=get(fa[x]);
}
void dfs(int rt,int x,int f){
siz[x]=1;//更新子树大小
root[x]=rt;//更新树根
for(int i=head[x];i;i=Next[i])
if(to[i]!=f){
int y=to[i];
father[y]=x;//更新真实父亲
v[y]=val[i];//更新通往父亲的边的编号
dep[y]=dep[x]+1;//更新深度
dfs(rt,y,x);
siz[x]+=siz[y];//更新子树大小
}
if(dep[x]<dep[get(x)]){//更换缩成的点的代表节点
int xx=get(x);//求出原来缩成的点的代表节点
fa[xx]=fa[x]=x;//更新缩成的点的代表结点
}
}
//get(x)表示找到x所在的缩成的点的代表节点
//father[x]表示x在树中的父亲
void add(int x,int y,int id){
if(siz[root[x]]<siz[root[y]])swap(x,y);
if(root[x]==root[y]){
r[id]=id;//更新答案
while(x!=y){
x=get(x),y=get(y);
if(x==y)break;
if(dep[x]<dep[y])swap(x,y);
if(dep[x]==dep[y]){
r[v[y]]=id;//更新其通往父亲节点的边的答案
father[y]=get(father[y]);//将father[y]更新为其被缩成的点的代表节点
fa[y]=father[y];//将fa[y]更新为被缩成的点的代表节点
y=father[y];//更新y
}
r[v[x]]=id;
father[x]=get(father[x]);
fa[x]=father[x];
x=father[x];
}
}else{
dep[y]=dep[x]+1;//更新y的深度
dfs(root[x],y,0);
addedge(x,y,id);//加边
addedge(y,x,id);
siz[root[x]]+=siz[y];
father[y]=x;v[y]=id;
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)scanf("%d%d",&x[i],&y[i]);
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++)fa[j]=root[j]=j,siz[j]=1,dep[j]=head[j]=0;
for(int j=1;j<=m;j++)r[j]=m+1;
for(int j=i;j<=m;j++)add(x[j],y[j],j);
for(int j=i;j<=m;j++)ans[j]+=m-r[j]+1;
}
for(int i=1;i<=m;i++)printf("%d
",ans[i]);
return 0;
}
我自己的代码
#include<bits/stdc++.h>
using namespace std;
#define N 1000005
struct nade{
int u,v;
}e[N];
int rt[N],Size[N],fathre[N],fa[N],la[N],dep[N],r[N],n,m,ans[N],head[N],Next[N],vet[N],edgenum,father[N],val[N];
void add(int u,int v,int id){
edgenum++;
Next[edgenum]=head[u];
head[u]=edgenum;
vet[edgenum]=v;
val[edgenum]=id;
}
int get(int u){
if(u==fa[u])return u;
return fa[u]=get(fa[u]);
}
void dfs(int s,int u,int faa){
rt[u]=s;Size[u]=1;
for(int e=head[u],v;e;e=Next[e])
if((v=vet[e])^faa){
father[v]=u;
la[v]=val[e];
dep[v]=dep[u]+1;
dfs(s,v,u);
Size[u]+=Size[v];
}
if(dep[u]<dep[get(u)]){
int now=get(u);
fa[now]=fa[u]=u;
}
}
void solve(int u,int v,int id){
if(Size[rt[u]]<Size[rt[v]])swap(u,v);
if(rt[u]==rt[v]){
r[id]=id;
while(u!=v){
u=get(u);v=get(v);
if(u==v)break;
if(dep[u]<dep[v])swap(u,v);
if(dep[u]==dep[v]){
r[la[v]]=id;
father[v]=get(father[v]);
fa[v]=father[v];
v=father[v];
}
r[la[u]]=id;
father[u]=get(father[u]);
fa[u]=father[u];
u=father[u];
}
}
else{
dep[v]=dep[u]+1;
dfs(rt[u],v,0);
add(u,v,id);
add(v,u,id);
Size[rt[u]]+=Size[v];
father[v]=u;la[v]=id;
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)scanf("%d%d",&e[i].u,&e[i].v);
for(int i=1;i<=m;i++){
edgenum=0;
for(int j=1;j<=n;j++){
fa[j]=rt[j]=j;
Size[j]=1;
dep[j]=head[j]=0;
}
for(int j=1;j<=m;j++)r[j]=m+1;
for(int j=i;j<=m;j++)solve(e[j].u,e[j].v,j);
for(int j=i;j<=m;j++)ans[j]+=m-r[j]+1;
}
for(int i=1;i<=m;i++)printf("%d
",ans[i]);
}