文字讲解
题目分析:
首先 ,要知道这道拓扑排序题目的性质。
食物链中的生物 —— 节点
生物之间的关系 —— 有向边
为了方便描述,我们
将 最左端是不会捕食其他生物的生产者 叫做 最佳生产者
将 最右端是不会被其他生物捕食的消费者 叫做 最佳消费者
数据中不会出现环
那么,“最大食物链”就是左端是 最佳生产者 ,右端是 最佳消费者
思路引导
易得,想要找到一条 最大食物链 ,则起始点入度要为0,终点出度要为0。于是有:
既要记录入度,还要记录出度!
现在的问题就是,如何找到所有的最大食物链的数量
正解
我们拿起笔,在草稿纸上先画一个图做参考。那么我们就拿样例进行举例吧。
(我先将最佳生产者表上蓝色,最佳消费者表上红色)
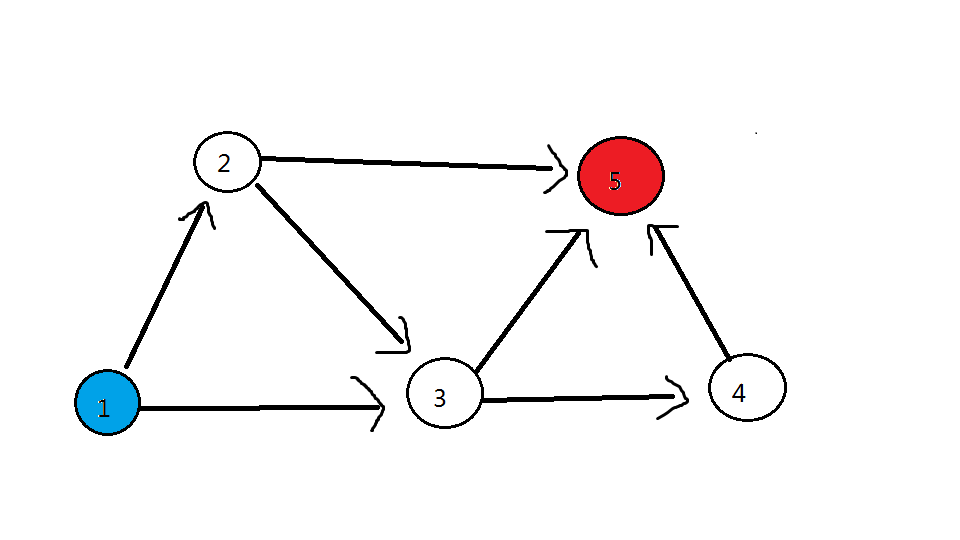
发现:答案为 到所有最佳消费者路径条数的总和
(这里的路径总和不是 连向它有几条边 ,而是以它结束的 最大食物链 数量的总和)
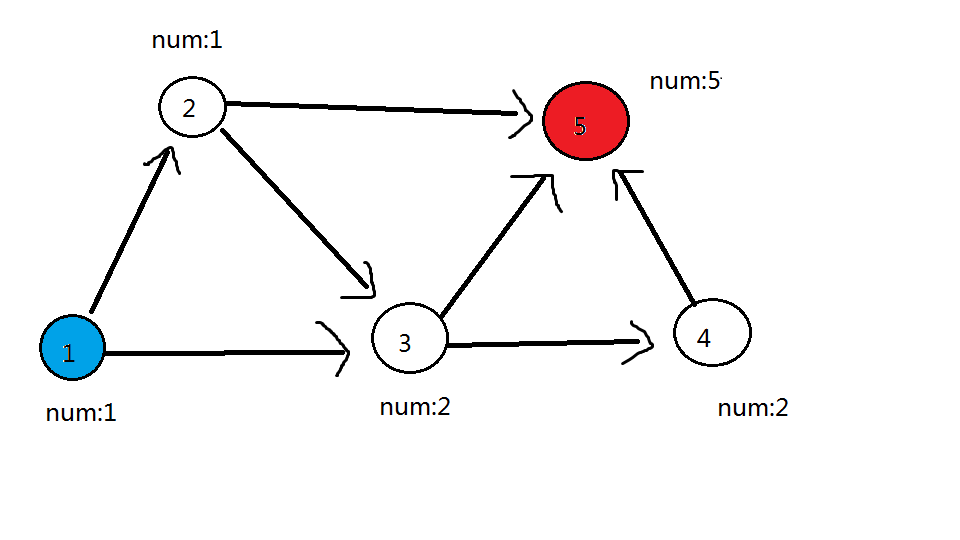
对于上面的图,(5) 号点的对应路径数量 取决于:以 到 (5) 号点的三个点( (2) 号、(3) 号、(4) 号) 结尾的 最大食物链个数 的总和。
而 以 (2) 号、(3) 号、(4) 号 结尾的 最大食物链个数 取决于:以 到达 (2) 号、(3)号、(4) 号 的点 结尾的 最大食物链个数 的总和。
以此类推,对于 以 任一点 结尾的 最大食物链的 数量,都取决于 蓝色点
各点数量对应关系在下图用绿色边标注
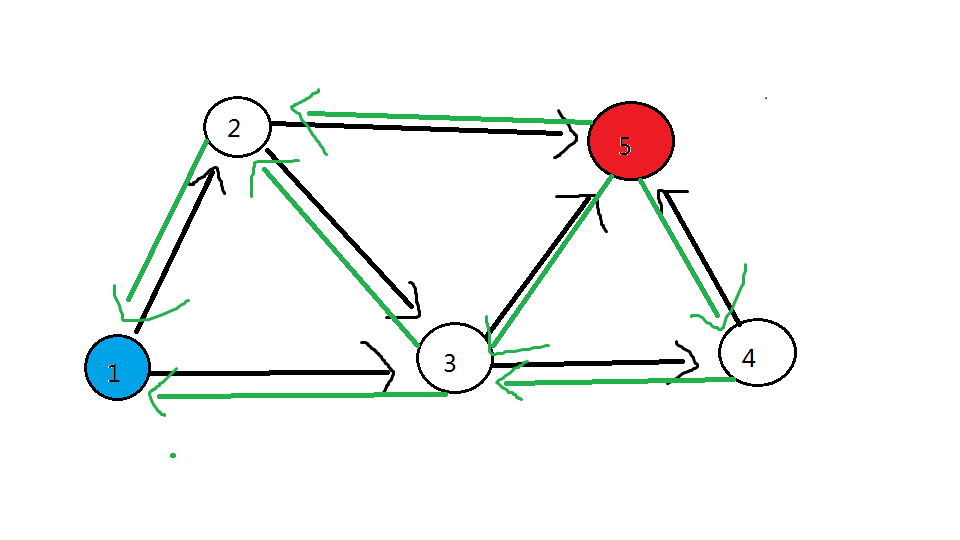
重点:
我们不妨使用拓扑排序,由题意得知 (Topo) 排序第一轮被删掉的点 一定是 蓝色点(最佳生产者),而 蓝色点 的答案为 (1)。
当第一轮删点时,将蓝色点可以到的点 的答案 都加上 蓝色点的 答案(即加 (1))。
即:拓扑排序 需要删除的点的答案 都累加到 它可以到达的点 上面去
最后累加所有 红色点(最佳消费者) 的答案,输出即可。
以第 i 个点结束的 最大食物链的 数量 = 以 指向第 i 个点的点 结尾的 最大食物链的 数量的和
以下是模拟操作过程:
加载时间较慢,请稍等
第一轮:删除 (1) 号蓝色点,(1) 号蓝色点可以到的点((2) 号点、(3) 号点)都加 (1)
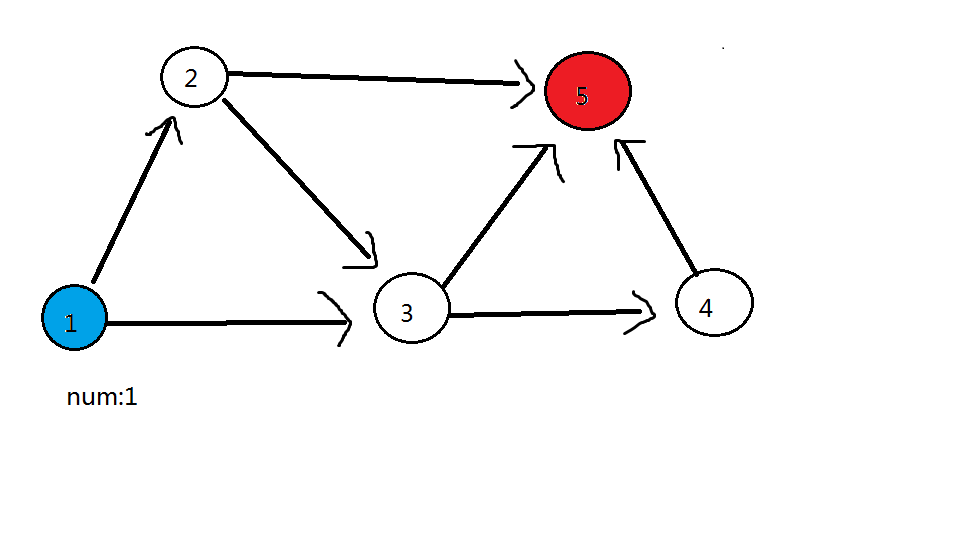
第二轮:删除 (2) 号点,(2) 号点可以到的点((3) 号点、(5) 号红色点)都加 (1)。此时 (3) 号点答案为 (2),(5) 号点答案为 (1)
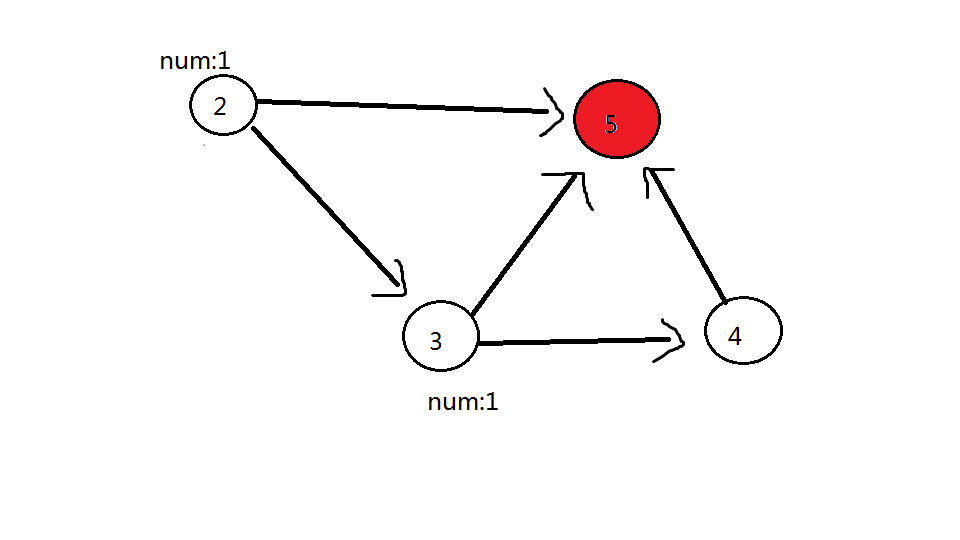
第三轮:删除 (3) 号点,(3) 号点可以到的点((4) 号点、(5) 号红色点)都加 (2)。此时 (5) 号点答案为 (3),(4) 号点答案为 (2)
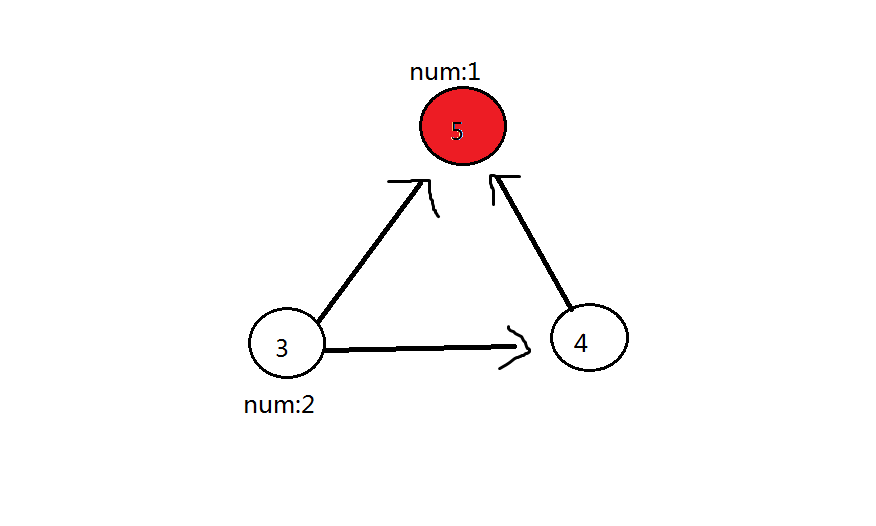
第四轮:最后删除 (4) 号点,(4) 号点可以到的点((5) 号红色点)加 (2),此时 (5) 号点答案为 (5)
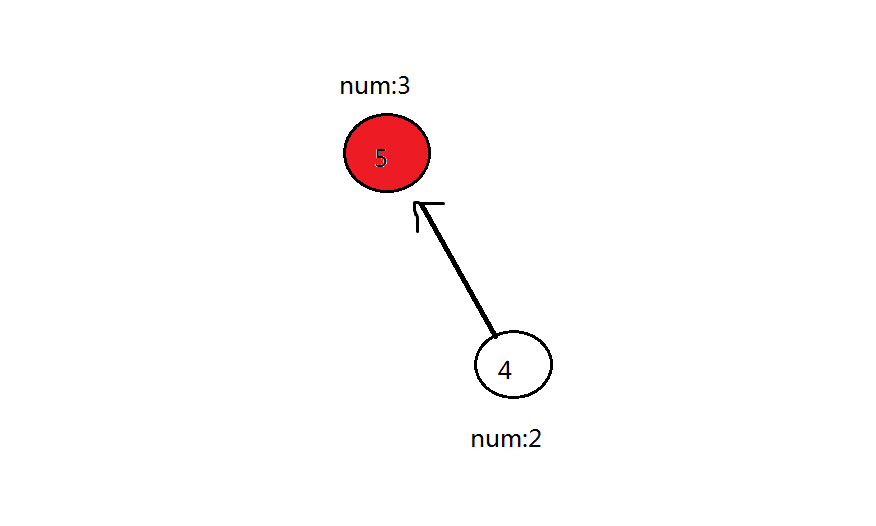
可见全图只有 (5) 号一个红色点,那么答案就是 (5) 号点的答案———— (5) 了
那么代码实现就很简单了!
上代码:
#include<bits/stdc++.h>//万能头,懒人必备
using namespace std;//标准名称函数库开启
const int MAXN = 5000 + 10;//定义常量大小
const long long mod = 80112002;//定义最终答案mod的值
int n,m;//n个点and边的关系数m
int in[MAXN];//记录每个点的入度
int out[MAXN];//记录每个点的出度
vector<int>nei[MAXN];//记录每个点相邻的点有哪些,用动态数组更加节省时间
queue<int>q;//拓扑排序模板队列
int ans;//答案
int num[MAXN];//记录到这个点的路径数量
inline int read(){//快速读入
int f = 1, x = 0;
char c = getchar();
while (c < '0' || c > '9')
{
if (c == '-')
f = -1;
c = getchar();
}
while (c >= '0' && c <= '9')
{
x = x * 10 + c - '0';
c = getchar();
}
return f * x;
}
int main(){//开始......
n = read(),m = read();//快速读入
for(int i = 1;i <= m; i++){//循环m条边
int x = read(),y = read();//输入左节点和右节点
in[y]++,out[x]++;//右节点入度+1,左节点出度+1
nei[x].push_back(y);//建立一条单向边
}
for(int i = 1;i <= n; i++){//初次寻找入度为0的点(最佳生产者)
if(in[i] == 0){//符合要求
num[i] = 1;//令到其的路径数量为1
q.push(i);//压入队列
}
}
while(!q.empty()){//只要还有入度为0的点
int tot = q.front();//取出首点
q.pop();//弹出
for(int i = 0;i < nei[tot].size(); i++){//枚举这个点相邻的所有点
int next = nei[tot][i]; //取出目前枚举到的点
in[next]--;//将这个点的入度-1(因为目前要删除第tot个点)
num[next] = (num[next] + num[tot]) % mod;//更新到next点的路径数量
if(in[next] == 0)q.push(nei[tot][i]);//如果这个点的入度为0了,那么压入队列
}
}
for(int i = 1;i <= n; i++){//寻找出度为0的点(最佳消费者)
if(out[i] == 0){//符合要求
ans = (ans + num[i]) % mod;//累加答案
}
}
cout<<ans<<"
";//输出
return 0;//end
}