[AGC006] D

Description

​ 现在有一个NN层的方块金字塔，从最顶层到最底层分别标号为1...N1...N。

​ 第ii层恰好有2i−12i−1个方块，且每一层的中心都是对齐的。

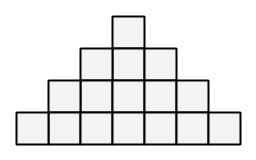
这是一个N=4N=4的方块金字塔

​ 现在，我们首先在最底层填入一个2N−12N−1的排列。之后，我们从i−1i−1层开始，逐步向上填入每一层的数。

​ 对于第ii（1≤i<N1≤i<N）层中位置为xx的方块，它的值为左下方、正下方和右下方的三个数的中位数。形式化地描述，就是i+1i+1层中x−1x−1、xx和x+1x+1三个位置的中位数。

​ 给定一个NN和长度为2N−12N−1的排列，请还原出最顶层唯一一个方块中的数值。

​ 下图就是一个还原的例子：

​

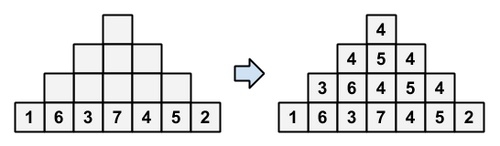
Input

​ 第一行一个正整数NN（2≤N≤1052≤N≤105）

​ 接下来一行有2N−12N−1个正整数a1,a2,...,a2N−1a1,a2,...,a2N−1，表示最底层的填数情况。保证aa是个排列。

Output

​ 只有一个正整数，表示最顶层那唯一一个格子里的数。

Sample Input

#Sample Input 1
4
1 6 3 7 4 5 2

#Sample Input 2
2
1 2 3

Sample Output

#Sample Output 1
4

#Sample Output 2
2

Sol

直接做显然是T的，我们考虑二分答案，二分之后把大于mid的置为1，其他置为0，然后从中间往两边判断，先出现俩连续0说明这个状态可行，否则不可行，如果没有连续数字的话直接判断第一位即可。

原因：两个连续相同的数字可以一直延伸到起点，而且水平距离近的优先。

Code

#include <cstdio>
int a[200005],n,ans;
bool dn(int x,int y,int z){return a[x]<=z&&a[y]<=z;}
bool up(int x,int y,int z){return a[x]>z&&a[y]>z;}
bool chk(int k)
{
    for(int i=0;i<n-1;i++)
    {
        if(up(n-i,n-i-1,k)||up(n+i,n+i+1,k)) return 0;
        if(dn(n-i,n-i-1,k)||dn(n+i,n+i+1,k)) return 1;
    }
    return dn(1,1,k);
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<n*2;i++) scanf("%d",&a[i]);
    for(int l=0,r=2*n-1,mid=(l+r)>>1;l<=r;mid=(l+r)>>1) if(chk(mid)) r=mid-1,ans=mid;else l=mid+1;
    printf("%d
",ans);
}