Print Article
Time Limit: 9000/3000 MS (Java/Others) Memory Limit: 131072/65536 K (Java/Others)
Total Submission(s): 3827 Accepted Submission(s): 1195
Problem Description
Zero has an old printer that doesn't work well sometimes. As it is antique, he still like to use it to print articles. But it is too old to work for a long time and it will certainly wear and tear, so Zero use a cost to evaluate this degree.
One day Zero want to print an article which has N words, and each word i has a cost Ci to be printed. Also, Zero know that print k words in one line will cost
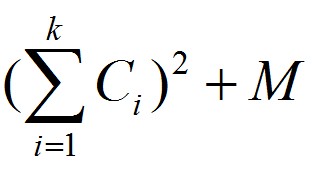
M is a const number.
Now Zero want to know the minimum cost in order to arrange the article perfectly.
One day Zero want to print an article which has N words, and each word i has a cost Ci to be printed. Also, Zero know that print k words in one line will cost
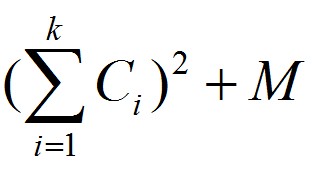
M is a const number.
Now Zero want to know the minimum cost in order to arrange the article perfectly.
Input
There are many test cases. For each test case, There are two numbers N and M in the first line (0 ≤ n ≤ 500000, 0 ≤ M ≤ 1000). Then, there are N numbers in the next 2 to N + 1 lines. Input are terminated by EOF.
Output
A single number, meaning the mininum cost to print the article.
Sample Input
5 5
5
9
5
7
5
Sample Output
230
Author
Xnozero
Source
Recommend
zhengfeng
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 5 using namespace std; 6 7 typedef long long int LL; 8 9 LL dp[550000],sum[550000],deq[650000]; 10 int n,m,s,t,e; 11 12 double slope(int i,int j) 13 { 14 return (double)(dp[i]+sum[i]*sum[i]-dp[j]-sum[j]*sum[j])/(sum[i]-sum[j]); 15 } 16 17 int main() 18 { 19 while(scanf("%d%d",&n,&m)!=EOF) 20 { 21 sum[0]=0; 22 for(int i=1;i<=n;i++) 23 { 24 scanf("%d",sum+i); 25 sum[i]+=sum[i-1]; 26 } 27 s=0; 28 for(int i=1;i<=n;i++) 29 { 30 if(sum[i]!=sum[s]) 31 { 32 s++; 33 sum[s]=sum[i]; 34 } 35 } 36 n=s; 37 s=0,e=0,dp[0]=0,deq[0]=0; 38 for(int i=1;i<=n;i++) 39 { 40 while(s<e&&slope(deq[s],deq[s+1])<=2*sum[i]) s++; 41 int j=deq[s]; 42 dp[i]=dp[j]+(sum[i]-sum[j])*(sum[i]-sum[j])+m; 43 while(s<e&&slope(deq[e-1],deq[e])>=slope(i,deq[e])) e--; e++; 44 deq[e]=i; 45 } 46 printf("%d ",dp[n]); 47 } 48 return 0; 49 }