【BZOJ3545】[ONTAK2010]Peaks
Description
在Bytemountains有N座山峰,每座山峰有他的高度h_i。有些山峰之间有双向道路相连,共M条路径,每条路径有一个困难值,这个值越大表示越难走,现在有Q组询问,每组询问询问从点v开始只经过困难值小于等于x的路径所能到达的山峰中第k高的山峰,如果无解输出-1。
Input
第一行三个数N,M,Q。
第二行N个数,第i个数为h_i
接下来M行,每行3个数a b c,表示从a到b有一条困难值为c的双向路径。
接下来Q行,每行三个数v x k,表示一组询问。
Output
对于每组询问,输出一个整数表示答案。
Sample Input
1 2 3 4 5 6 7 8 9 10
1 4 4
2 5 3
9 8 2
7 8 10
7 1 4
6 7 1
6 4 8
2 1 5
10 8 10
3 4 7
3 4 6
1 5 2
1 5 6
1 5 8
8 9 2
Sample Output
1
-1
8
HINT
【数据范围】
N<=10^5, M,Q<=5*10^5,h_i,c,x<=10^9。
【BZOJ3551】[ONTAK2010]Peaks加强版
题意:同3545,强制在线
题解:3545:这道题我们很容易想到用最小生成树,然后离线来搞。将询问按照x排序,在最小生成树加边的过程中,每加一条边就把所有x小于当前边权的询问处理掉。求第k大可以用Treap搞定,将并查集合并时也将Treap进行启发式合并(把小的Treap暴力拆掉,一个一个加到大的中去),不过我有点懒得写了。
3551:既然是强制在线我们就不能用Treap搞了,但最小生成树是一定要求的。本题利用到了Kruskal重构树的性质(什么是Kurskal重构树?)
在并查集合并的时候,我们不直接令f[a]=b,而是新建一个点ext,将a和b都合并到以ext为根的并查集上,并且令ext的点权等于e(a,b)的边权,这样我们就得到了一棵Kruskal重构树,本题的Kruskal重构树如下图所示
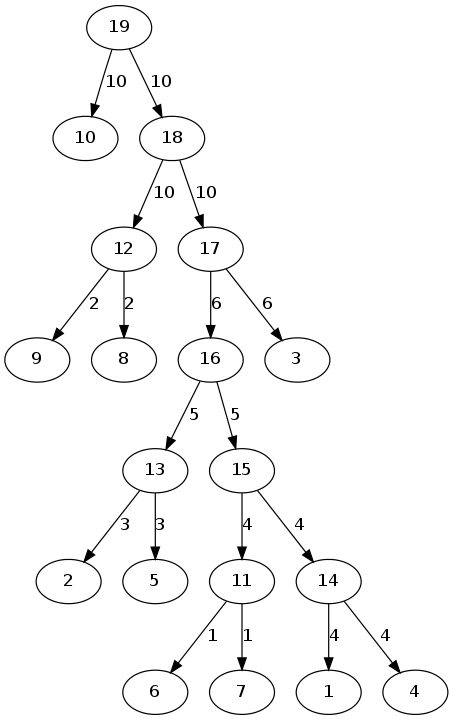
容易发现,Kruskal重构树满足:子节点的边权一定小于父亲节点的边权。于是我们可以用倍增求出v的深度最小的、且满足边权不超过x的祖先,因此满足所有到v路径上最大边权不超过x的节点,一定就在这棵子树上,然后询问就变成了求这棵子树中的第k大。为此我们只需要用DFS序,然后就可以将求子树的第k大转变成求一段区间中的第k大,这样跑一遍主席树就行了。
再捋一下思路:先离散化(因为是10^9),在跑Kruskal,顺便建树,然后预处理倍增,求出DFS序,再预处理主席树,最后在线处理询问
由于本人比较懒我就直接用3551的代码改一改就把3545交了,但其实写一发Treap也是挺好的
至于TLE的建议写个读入优化吧,没准就AC了。
3551代码:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn=200010;
int n,m,Q,cnt,tot,sum,H,ans;
struct edge
{
int pa,pb,len;
}p[500010];
struct node
{
int siz,ls,rs;
}s[4000000];
struct NUM
{
int num,org;
}v[maxn];
int h[maxn],f[maxn],bel[maxn],fa[maxn][20],dp[maxn][20],Log[maxn],to[maxn],next[maxn],root[maxn];
int qx[maxn],qy[maxn],qz[maxn],ql[maxn],qr[maxn],q[maxn],rx[maxn],rh[maxn],head[maxn];
bool cmp1(edge a,edge b)
{
return a.len<b.len;
}
bool cmp2(NUM a,NUM b)
{
return a.num<b.num;
}
int readin()
{
int ret=0,f=1; char gc=getchar();
while(gc<'0'||gc>'9'){if(gc=='-')f=-f; gc=getchar();}
while(gc>='0'&&gc<='9') ret=ret*10+gc-'0',gc=getchar();
return ret*f;
}
int find(int x)
{
if(f[x]!=x) f[x]=find(f[x]);
return f[x];
}
void add(int a,int b)
{
if(b==0) return ;
to[cnt]=b;
next[cnt]=head[a];
head[a]=cnt++;
}
void dfs(int x)
{
ql[x]=q[0];
if(head[x]==-1) q[++q[0]]=x;
for(int i=head[x];i!=-1;i=next[i]) dfs(to[i]);
qr[x]=q[0];
}
void RMQ()
{
int i,j;
for(i=2;i<=2*n;i++) Log[i]=Log[i>>1]+1;
for(j=1;(1<<j)<=2*n;j++)
for(i=1;i+(1<<j)-1<=2*n;i++)
fa[i][j]=fa[fa[i][j-1]][j-1];
}
void insert(int x,int &y,int l,int r,int pos)
{
y=++tot;
if(l==r)
{
s[y].siz=s[x].siz+1;
return ;
}
int mid=l+r>>1;
if(pos<=mid) s[y].rs=s[x].rs,insert(s[x].ls,s[y].ls,l,mid,pos);
else s[y].ls=s[x].ls,insert(s[x].rs,s[y].rs,mid+1,r,pos);
s[y].siz=s[s[y].ls].siz+s[s[y].rs].siz;
}
void query(int x,int y,int l,int r,int pos)
{
if(l==r)
{
ans=rh[l];
return ;
}
int mid=l+r>>1;
if(s[s[y].rs].siz-s[s[x].rs].siz>=pos) return query(s[x].rs,s[y].rs,mid+1,r,pos);
return query(s[x].ls,s[y].ls,l,mid,pos-s[s[y].rs].siz+s[s[x].rs].siz);
}
int main()
{
n=readin(),m=readin(),Q=readin();
memset(head,-1,sizeof(head));
int i,j,a,b,c;
for(i=1;i<=n;i++) v[i].num=readin(),v[i].org=i;
sort(v+1,v+n+1,cmp2);
rh[H]=-1;
for(i=1;i<=n;i++)
{
if(rh[H]<v[i].num) rh[++H]=v[i].num;
h[v[i].org]=H;
}
for(i=1;i<=m;i++) p[i].pa=readin(),p[i].pb=readin(),p[i].len=readin();
sort(p+1,p+m+1,cmp1);
for(i=1;i<2*n;i++) f[i]=i;
for(i=1;i<=m;i++)
{
a=find(p[i].pa),b=find(p[i].pb);
if(a!=b)
{
sum++;
add(sum+n,a),add(sum+n,b);
f[a]=f[b]=sum+n;
fa[a][0]=fa[b][0]=sum+n;
rx[sum]=p[i].len;
if(sum==n-1) break;
}
}
dfs(sum+n);
for(i=1;i<=n;i++) insert(root[i-1],root[i],1,H,h[q[i]]);
RMQ();
for(i=1;i<=Q;i++)
{
scanf("%d%d%d",&a,&b,&c);
a^=ans,b^=ans,c^=ans;
int temp=a;
for(j=Log[2*n];j>=0;j--)
if(fa[temp][j]&&rx[fa[temp][j]-n]<=b)
temp=fa[temp][j];
if(c>qr[temp]-ql[temp])
{
printf("-1
");
ans=0;
continue;
}
query(root[ql[temp]],root[qr[temp]],1,H,c);
printf("%d
",ans);
}
return 0;
}