【BZOJ2956】模积和 分块

【BZOJ2956】模积和

Description

　求∑∑((n mod i)*(m mod j))其中1<=i<=n,1<=j<=m,i≠j。

Input

第一行两个数n,m。

Output

　　一个整数表示答案mod 19940417的值

Sample Input

3 4

Sample Output

1

样例说明
　　答案为(3 mod 1)*(4 mod 2)+(3 mod 1) * (4 mod 3)+(3 mod 1) * (4 mod 4) + (3 mod 2) * (4 mod 1) + (3 mod 2) * (4 mod 3) + (3 mod 2) * (4 mod 4) + (3 mod 3) * (4 mod 1) + (3 mod 3) * (4 mod 2) + (3 mod 3) * (4 mod 4) = 1

数据规模和约定
　　对于100%的数据n,m<=10^9。

题解：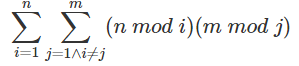

推到这之后发现有个i²不好搞，但是我们有平方和定理

然后分块就好了

脏脏的从黄学长的博客和百度上扒了图片，又直接扒了6的乘法逆元，不要打我~

#include <cstdio>
#include <cstring>
#include <iostream>
#define mod 19940417ll
#define m6 3323403ll
//6的逆元
using namespace std;
typedef long long ll;
ll n,m,i,last,ans;
ll s1,s2,s3;
ll pm(ll x,ll y)
{
	ll z=1;
	while(y)
	{
		if(y&1)	z=(z*x)%mod;
		x=(x*x)%mod,y>>=1;
	}
	return z;
}
ll sum(ll x)
{
	return x*(x+1)%mod*(2*x+1)%mod*m6%mod;
}
int main()
{
	scanf("%lld%lld",&n,&m);
	if(n>m)	swap(n,m);
	for(i=1;i<=n;i=last+1)
	{
		last=n/(n/i);
		s1+=((last-i+1)*n-(i+last)*(last-i+1)/2%mod*(n/i)%mod+mod)%mod;
		s1%=mod;
	}
	for(i=1;i<=m;i=last+1)
	{
		last=m/(m/i);
		s2+=((last-i+1)*m-(i+last)*(last-i+1)/2%mod*(m/i)%mod+mod)%mod;
		s2%=mod;
	}
	for(i=1;i<=n;i=last+1)
	{
		last=min(n/(n/i),m/(m/i));
		s3+=(last-i+1)*n%mod*m%mod;
		s3-=(i+last)*(last-i+1)/2%mod*((n/i)*m%mod+(m/i)*n%mod)%mod;
		s3+=(n/i)*(m/i)%mod*(sum(last)-sum(i-1)+mod)%mod;
		s3%=mod;
	}
	ans=(s1*s2%mod-s3+mod)%mod;
	printf("%lld",ans);
	return 0;
}