lowbit(x) = x & (-x)即取x得二进制最右边的1和它右边所有的0,lowbit(x)也可以理解为能整除x的最大2的幂次。
树状数组及其应用
先看一个问题:给出一个整数序列A,元素个数为N(N <= 100000),接下来查询K次(K <= 100000),每次查询将给出一个正整数x(x <= N),求前x个整数之和。
对于这个问题,一般的做法是开一个sum数组,其中sun[i]表示前i个整数之和(数组下标从1开始),这样sun数组就可以在输入N个整数时就预处理出来。接着每次查询前x个整数之和时,输出sun[x]即可。显然每次查询的复杂度是O(1),因此查询的总复杂度是O(K)。
升级一下这个问题:假设查询过程中可能随时给第x个整数加上一个整数v,要求在查询中能实时输出前x个整数之和(更新操作和查询操作的次数总和为K次)。
我们可以考虑用树状数组解决上述问题
树状数组其实就是一个数组,并且与sum数组类似,是一个用来记录和的数组,只不过它存放的不是前i个整数之和,而是在i号位之前(含i号位,下同)lowbit(i)个整数之和。数组A是原始数组,有A[1] ~ A[8]共8个元素;数组C是树状数组,其中C[i]存放数组A中i号位之前lowbit(i)个元素之和。显然C[i]的覆盖长度是lowbit(i)。
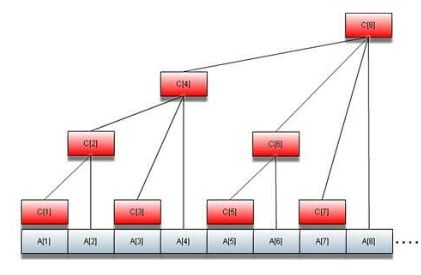
C[1]到C[8]的定义:
C[1] = A[1] (长度为 lowbit(1) = 1)
C[2] = A[1] + A[2] (长度为 lowbit(2) = 2)
C[3] = A[3] (长度为lowbit(3) = 1)
C[4] = A[1] + A[2] + A[3] + A[4] (长度为lowbit(4) = 4)
C[5] = A[5] (长度为lowbit(5) = 1)
C[6] = A[6] (长度为lowbit(6) = 2)
C[7] = A[7] (长度为lowbit(7) = 1)
C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8] (长度为lowbit(8) = 8)
(1)设计函数getSum(x),返回前x个数之和A[1] + ...... + A[x]
(2)设计函数update(x),将实现将第x个数加上一个数v的功能,即A[x] += v;
此处强调,树状数组的定义非常重要,特别是“C[i]的覆盖长度是lowbit(i)”这点:另外,树状数组的下标必须从1开始。
记sum(1, x) = A[1] + ...... + A[x],由于C[x]的覆盖长度为lowbit(x),因此:C[x] = A[x - lowbit(x) + 1] + .... + A[x]
于是可以马上得到
sum(1, x) = A[1] + ....... + A[x]
= A[1] + ....... + A[x - lowbit(x)] + A[x - lowbit(x) + 1] + ...... + A[x]
= sum(x, x - lowbit(x)) + C[x]
这样就可以吧sum(1, x)转换为sum(1, x - lowbit(x))了,下面就是getSum函数:
1 //getSum函数返回前x个整数之和 2 int getSum(int x) 3 { 4 int sum = 0;//记录和 5 for(int i = x; i > 0; i -= lowbit(i))//注意i > 0而不是 i >= 0 6 { 7 sum += c[i];//累计c[i],然后把问题缩小为sum(1, i - lowbit(i)) 8 } 9 return sum; 10 }
显然,由于lowbit(i)的作用是定位i的二进制最右边的1,因此i = i - lowbit(i)事实上是不断把i的二进制中最右边的1置为0的过程。另外如果要求数组下标在区间[x, y]内的数之和,即A[x] + A[x + 1] + ..... _ A[y],可以转换为getSum(y) - getSum(x - 1)来解决。

想要给A[x]加上v时,怎么去寻找树状数组的对应项呢?
要让A[x]加上v,就是要寻找树状数组C中能覆盖A[x]的那些元素,让它们都加上v。只需要总是寻找离当前的“矩形”C[x]最近的“矩形”C[y],使得C[y]能够覆盖C[x]即可。
如何找到距离当前的C[x]最近的能覆盖C[x]的C[y]呢?首先,可以得到一个结论:lowbit(y)必须大于low(x)(不然无法进行覆盖)。于是问题等价为求一个尽可能小的整数a,使得lowbit(x + a) > lowbit(x)。显然,由于lowbit(x)是取x的二进制最右边的1的位置,因此如果lowbit(a) < lowbit(x),lowbit(x + a) < lowbit(x)。因此,lowbit(a)必须不小于lowbit(x)。当a取lowbit(x)时,由于x和a的二进制最右边1的位置相同,因此x + a会在这个1的位置上产生进位,使得进位过程中所有连续的1变为0,直到把它左边第一个0置为1结束。于是lowbit(x + a) > lowbit(x)显然成立,最小的a 就是lowbit(x)。
1 //update函数将第x个整数加上v 2 void update(int x, int v) 3 { 4 for(int i = x; i <= N; i += lowbit(i))//注意i必须能取到N 5 { 6 c[i] += v;//让c[i]加上v,然后让c[i + lowbit(i)]加上v 7 } 8 }
问题描述:
给定一个有N个正整数的序列A(N <= 100000,A[i] <= 100000),对序列中的每个数,求出序列中它左边比它小的数的个数。
使用hash数组的做法:其中hash[x]记录整数x当前出现的次数。接着,从左到右遍历序列A,假设当前访问的是A[i],那么就另hash[A[i]]加1,表示当前A[i]的出现次数增加了一次。同时,序列中在A[i]左边比A[i]小的数的个数等于hash[1] + hash[2] + .... + hash[A[i] - 1],这个和需要输出。但是很显然,这两个工作可以通过树状数组的update(A[i], i)和getSum(A[i] - 1)来解决。
使用树状数组时,不需要建立一个hash数组,它只存在于逻辑中
1 #include<cstdio> 2 #include<cstring> 3 const int maxn = 10010; 4 #define lowbit(i) ((i) & (-i))//lowbit写成宏定义的形式,注意括号 5 6 int c[maxn];//树状数组 7 //update函数将第x个整数加上v 8 void update(int x, int v) 9 { 10 for(int i = x; i < maxn; i += lowbit(i))//i < maxn 或者 i <= n都可以 11 { 12 c[i] += v; 13 } 14 } 15 16 //getSum函数返回前x个整数之和 17 int getSum(int x) 18 { 19 int sum = 0; 20 for(int i = x; i > 0; i -= lowbit(i)) 21 { 22 sum += c[i]; 23 } 24 return sum; 25 } 26 27 int main() 28 { 29 int n, x; 30 scanf("%d", &n); 31 memset(c, 0, sizeof(0));//树状数组初值为0 32 for(int i = 0; i < n; i++) 33 { 34 scanf("%d", &x);//输入序列元素 35 update(x, 1);//x的出现次数加1 36 printf("%d ", getSum(x - 1));//查询当前小于x的数的个数 37 } 38 return 0; 39 }
统计序列中在元素左边比该元素大的元素个数相当于计算hash[A[i] + 1] + ..... + hash[N],于是getSum(N) - getSum(A[i])就是答案。
当A[i] <= N不成立呢(例如A[i] <= 1000000000)。例如:序列A为{520,999999999,18,666,88888},如果仅考虑它们的大小关系,那么这个序列和{2,5,1,3,4}是等价的。因此要做的是将A[i]与1~N对应起来,而这与“给定N个学生的分数,给他们进行排名,分数相同则排名相同”显然是同一种问题。一般来说,可以设置一个临时的结构体数组,用以存放输入的序列元素的值以及原始序号,而在输入完毕后将数组按val从小到大进行排序,排序完再按照“计算排名”的方式将“排名”根据原始序号pos存入一个新的数组即可。由于这种做法可以把任何不在合适区间的整数或者非整数都转换为不超过元素个数大小的整数,因此一般把这种技巧称为离散化。
下面是针对“统计序列中在元素左边比该元素小的元素个数”的问题给出使用离散化的代码:
1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 using namespace std; 5 const int maxn = 100010; 6 #define lowbit(i) ((i) & (-i))//lowbit写成宏定义的形式,注意括号 7 8 struct Node{ 9 int val;//序列元素的值 10 int pos;//原始序号 11 }temp[maxn];//temo数组临时存放输入数据 12 13 int A[maxn];//离散化后的原始数组 14 int c[maxn];//树状数组 15 16 //update函数将第x个整数加上v 17 void update(int x, int v) 18 { 19 for(int i = x; i < maxn; i += lowbit(i))//i < maxn 或者 i <= n都可以 20 { 21 c[i] += v;//让c[i]加上v,然后让c[i + lowbit(i)]加上v 22 } 23 } 24 25 //getSum函数返回前x个整数之和 26 int getSum(int x) 27 { 28 int sum = 0;//记录和 29 for(int i = x; i > 0; i -= lowbit(i))//注意是 i > 0而不是 i >= 0 30 { 31 sum += c[i];//累计c[i],然后把问题缩小为sum[1, i - lowbit(i)] 32 } 33 return sum;//返回和 34 } 35 36 //按val从小到大排序 37 bool cmp(Node a, Node b) 38 { 39 return a.val < b.val; 40 } 41 42 int main() 43 { 44 int n; 45 scanf("%d", &n); 46 memset(c, 0, sizeof(c));//树状数组初值为0 47 for(int i = 0; i < n; i++) 48 { 49 scanf("%d", &temp[i].val);//输入序列元素 50 temp[i].pos = i;//原始序号 51 } 52 //离散化 53 sort(temp, temp + n, cmp);//按val从小到大排序 54 for(int i = 0; i < n; i++) 55 { 56 //与上一个元素值不同时,赋值为元素个数 57 if(i == 0 || temp[i].val != temp[i - 1].val) 58 { 59 A[temp[i].pos] = i + 1;//注意这里必须从1开始 60 } 61 else//与上一元素值相同时,直接继承 62 { 63 A[temp[i].pos] = A[temp[i - 1].pos]; 64 } 65 } 66 //正式进入更新和求和操作 67 for(int i = 0; i < n; i++) 68 { 69 update(A[i], 1);//A[i]的出现次数加1 70 printf("%d ", getSum(A[i] - 1));//查询当前小于A[i]的数的个数 71 } 72 return 0; 73 }
一般来说,离散化只适用于离线查询,因为必须知道所有出现的元素之后才能方便进行离散化。但是对在线查询来说也不是一点办法没有,也可以先把所有操作记录下来,然后对其中出现的数据进行离散化,之后按照记录下来的操作顺序正常“在线”查询即可。
树状数组求解序列第K大的问题
对一个数列来说,如果用hash数组记录每个元素出现的个数,那么序列第K大就是在求最小的i,使得hash[1] + ..... + hash[i] >= k成立。也就是说,如果用树状数组来解决hash数组的求和问题,那么这个问题就等价于寻找第一个满足条件“getSum(i) >= k”的i。
针对这个问题,由于hash数组的前缀和是递增的。可以令l = 1、r = MAXN,然后在[1, r]范围内进行二分,对当前的mid,判断getSum(mid) >= k是否成立:如果成立,说明所求位置不超过mid,因此令r = mid;如果不成立,说明所求位置大于mid,因此令 l = mid + 1.如此二分,直到 l < r 不成立为止。
1 //求序列元素第K大 2 int findKthElement(int K) 3 { 4 int l = 1, r = MAXN, mid;//初始区间[1, MAXN] 5 while(l < r)//循环,直到[1,r]能锁定单一元素 6 { 7 mid = (1 + r) / 2; 8 if(getSum(mid) >= K)//所求位置不超过mid 9 r = mid; 10 else//所求位置大于mid 11 l = mid + 1; 12 } 13 return l;//返回二分夹出的元素 14 }
如果想求A[a][b] ~ A[x][y]这个子矩阵的元素之和,只需计算getSum(x, y) - getSum(x - 1, y) - getSum(x, y -1) + getSum(x - 1, y - 1)即可。更高维的情况只需要把for循环改为相应的重数即可。二维树状数组的代码如下所示:
1 int c[maxn][maxn];//二维树状数组 2 //二维update函数位置为(x, y)的整数加上v 3 void update(int x, int y, int v) 4 { 5 for(int i = x; i < maxn; i += lowbit(i)) 6 { 7 for(int j = y; j < maxn; j += lowbit(j)) 8 { 9 c[i][j] += v; 10 } 11 } 12 } 13 14 //二维getSum函数返回(1, 1)到(x, y)的子矩阵中元素之和 15 int getSum(int x, int y) 16 { 17 int sum = 0; 18 for(int i = x; i > 0; i -= lowbit(i)) 19 { 20 for(int j = y; j > 0; j -= lowbit(j)) 21 { 22 sum += c[i][j]; 23 } 24 } 25 return sum; 26 }
树状数组的区间更新和单点查询
(1)设计函数getSum(x),返回A[x].
(2)设计函数update(x, v),将A[1] ~ A[x]的每个数都加上一个数v。
要想对树状数组的区间进行更新和单点查询需要对树状数组的定义进行修改。
首先,树状数组C中每个“矩形”C[i]仍然保持和之前一样的长度,即lowbit(i),只不过C[i]不在表示这段区间的元素之和,而是表示这段区间每个数当前被加了多少。这样A[x]的值就是覆盖它的若干个矩形C[i]的元素之和。也就是以前的update函数
1 //getSum函数返回第x个整数的值 2 int getSum(int x) 3 { 4 int sum = 0;//记录和 5 for(int i = x; i < maxn; i += lowbit(i))//沿着i增大的路径 6 { 7 sum += c[i];//累计c[i] 8 } 9 return sum;//返回和 10 }
1 //update函数将前x个函数都加上v 2 void update(int x, int v) 3 { 4 for(int i = x; i > 0; i -= lowbit(i))//沿着i减小的路径 5 { 6 c[i] += v;//让c[i]加上v 7 } 8 }
显然,如果需要让A[x] ~ A[y]的每个数都加上v,只要让A[1] ~ A[y]的每个数加上v,然后让A[1] ~ A[x - 1]的每个数加上-v即可,即先后执行update(y, v)与update(x - 1, -v)。
摘自《算法笔记》