参考文章:
http://blog.csdn.net/runninghui/article/details/8905019
http://blog.csdn.net/u013795055/article/details/38599321
http://blog.csdn.net/g_congratulation/article/details/52734306
快速幂:
求幂时最朴素的方法就是循环n次进行求解,这样得到的是复杂度为O(n)的算法,还有一种比较优化的方法就是 ,一直这样递归下去,就可以省去部分计算,这样的时间复杂度约为O(logn);
,一直这样递归下去,就可以省去部分计算,这样的时间复杂度约为O(logn);
快速幂是一种用二进制方法求幂的运算
比如说: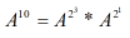 (注意:10的二进制表示法为:1010,分别对应A的次幂)
(注意:10的二进制表示法为:1010,分别对应A的次幂)
1 while(n) 2 { 3 if(n & 1) 4 { 5 ans *= matex; 6 } 7 matex = matex * matex; 8 n >> 1; 9 }
矩阵相乘
//O(n^3)算法 #include <iostream> #include <cstdio> #include <cstring> #include <cstdlib> #include <cmath> #include <algorithm> using namespace std; #define LL __int64 #define MOD 1000 typedef struct MATRIX { int mat[50][50]; }MATRIX; MATRIX mat_multiply (MATRIX a,MATRIX b,int n) { MATRIX c; //c[i][j]= Σ a[i][k]*b[k][j] memset(c.mat,0,sizeof(c.mat)); /* for(int i=0;i<n;i++) //a矩阵一行一行往下 for(int j=0;j<n;j++) //b矩阵一列一列往右 for(int k=0;k<n;k++) //使a矩阵 第i行第k个元素 乘以 b矩阵 第j列第k个元素 if(a[i][k] && b[k][j]) //剪枝(添条件,设门槛),提高效率,有一个是0,相乘肯定是0 c.mat[i][j]+=a.mat[i][k]*b.mat[k][j]; */ //上面也是可以的,但是下面的剪枝更好一些,效率更高一些,但是运算顺序有点难想通,,, //上面就是C[i][j]一次就求出来,下面就是每次c[i][j]求出一项【就是上面红体字,每次各求一列】 for(int k=0;k<n;k++) //这个可以写到前面来, for(int i=0;i<n;i++) if(a.mat[i][k]) //剪枝:如果a.mat[i][k]是0,就不执行了 for(int j=0;j<n;j++) if(b.mat[k][j]) //剪枝:如果b.mat[i][k]是0,就不执行了 { c.mat[i][j]+=a.mat[i][k]*b.mat[k][j]; if(c.mat[i][j]>=MOD) //这个看实际需求,要不要取模 c.mat[i][j]%=MOD; //取模的复杂度比较高,所以尽量减少去模运算,添加条件,只有当大于等于MOD的时候才取余 } return c; } int main()//这个只是用来测试用的。。。 { int n; MATRIX A,B,C; memset(A.mat,0,sizeof(A.mat)); memset(B.mat,0,sizeof(B.mat)); memset(C.mat,0,sizeof(C.mat)); scanf("%d",&n); //矩阵规模,这里是方阵,行数等于列数 for(int i=0;i<n;i++) //初始化A矩阵 for(int j=0;j<n;j++) scanf("%d",&A.mat[i][j]); for(int i=0;i<n;i++) //初始化B矩阵 for(int j=0;j<n;j++) scanf("%d",&B.mat[i][j]); C=mat_multiply (A,B,n); for(int i=0;i<n;i++) //打印C矩阵 { for(int j=0;j<n;j++) printf("%3d",C.mat[i][j]); printf(" "); } return 0; }
矩阵快速幂
矩阵快速幂的核心思想与快速幂基本一致。
1 //矩阵快速幂 2 #include <iostream> 3 #include <cstdio> 4 #include <cstring> 5 #include <cstdlib> 6 #include <cmath> 7 #include <algorithm> 8 using namespace std; 9 #define LL __int64 10 #define MOD 1000 11 typedef struct MATRIX 12 { 13 int mat[50][50]; 14 }MATRIX; 15 16 MATRIX mat_multiply (MATRIX a,MATRIX b,int n) 17 { 18 MATRIX c; //c[i][j]= Σ a[i][k]*b[k][j] 19 memset(c.mat,0,sizeof(c.mat)); 20 for(int k=0;k<n;k++) 21 for(int i=0;i<n;i++) 22 if(a.mat[i][k]) 23 for(int j=0;j<n;j++) 24 if(b.mat[k][j]) 25 { 26 c.mat[i][j]+=a.mat[i][k]*b.mat[k][j]; 27 if(c.mat[i][j]>=MOD) 28 c.mat[i][j]%=MOD; 29 } 30 return c; 31 } 32 33 MATRIX mat_quick_index(MATRIX a,int N,int n) 34 { 35 MATRIX E; //单位矩阵,就像数值快速幂里,把代表乘积的变量初始化为1 36 37 // memset(E.mat,0,sizeof(E.mat)); //置零,单位矩阵除了主对角线都是1,其他都是0 38 // for(int i=0;i<n;i++) //初始化单位矩阵【就是主对角线全是1】 39 // E.mat[i][i]=1; 40 41 for(int i=0;i<n;i++) 42 for(int j=0;j<n;j++) 43 E.mat[i][j]=(i==j); //酷炫*炸天的初始化!!! 44 45 while(N>0) 46 { 47 if(N & 1) 48 E=mat_multiply(E,a,n); 49 N>>=1; 50 a=mat_multiply(a,a,n); 51 } 52 return E; 53 } 54 55 int main() 56 { 57 int n,N; //n为矩阵(方阵)规模,几行,N为指数 58 MATRIX A,C; 59 60 memset(A.mat,0,sizeof(A.mat)); 61 memset(C.mat,0,sizeof(C.mat)); 62 63 scanf("%d",&n); //矩阵规模,这里是方阵,行数等于列数 64 65 for(int i=0;i<n;i++) //初始化A矩阵 66 for(int j=0;j<n;j++) 67 scanf("%d",&A.mat[i][j]); 68 69 scanf("%d",&N); 70 C=mat_quick_index(A,N,n); 71 72 for(int i=0;i<n;i++) //打印C矩阵 73 { 74 for(int j=0;j<n;j++) 75 printf("%3d",C.mat[i][j]); 76 printf(" "); 77 } 78 return 0; 79 }
矩阵快速幂优化递推式:斐波那契数列
单位矩阵:除对角线为1外,其余均为0
矩阵乘法与递推式之间的关系:
在斐波那契数列中:

即
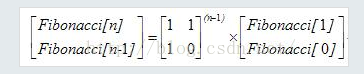
用矩阵快速幂求斐波那契数列的第N项的代码:
1 #include<cstdio> 2 #include<algorithm> 3 #include<string> 4 #include<iostream> 5 using namespace std; 6 7 const int M = 1e9+7; 8 9 struct Matrix{ 10 long long a[2][2]; 11 Matrix(){ 12 memset(a, 0, sizeof(a)); 13 } 14 Matrix operator *(const Matrix y) 15 { 16 Matrix ans; 17 for(int i = 0; i <= 1; i++) 18 { 19 for(int j = 0; j <= 1; j++) 20 { 21 for(int k = 0; k <= 1; k++) 22 { 23 ans.a[i][j] += a[i][k] * y.a[k][j]; 24 } 25 } 26 } 27 28 for(int i = 0; i <= 1; i++) 29 { 30 for(int j = 0; j <= 1; j++) 31 { 32 ans.a[i][j] %= M; 33 } 34 } 35 return ans; 36 } 37 38 void operator = (const Matrix b) 39 { 40 for(int i = 0; i <= 1; i++) 41 { 42 for(int j = 0; j <= 1; j++) 43 { 44 a[i][j] = b.a[i][j]; 45 } 46 } 47 } 48 }; 49 50 int solve(long long x) 51 { 52 Matrix ans, trs; 53 ans.a[0][0] = ans.a[1][1] = 1; 54 trs.a[0][0] = trs.a[1][0] = trs.a[0][1] = 1; 55 while(x) 56 { 57 if(x & 1) 58 { 59 ans = ans * trs; 60 } 61 trs = trs * trs; 62 x >>= 1; 63 } 64 return ans.a[0][0]; 65 } 66 67 int main() 68 { 69 int n; 70 scanf("%d", &n); 71 cout << solve(n-1) << endl; 72 return 0; 73 }