0 - 背景
0.0 - 为什么需要字典学习?
这里引用这个博客的一段话,我觉得可以很好的解释这个问题。
回答这个问题实际上就是要回答“稀疏字典学习 ”中的字典是怎么来的。做一个比喻,句子是人类社会最神奇的东西,人类社会的一切知识无论是已经发现的还是没有发现的都必然要通过句子来表示出来(从某种意义上讲,公式也是句子)。这样说来,人类懂得的知识可要算是极为浩繁的。有人统计过人类每天新产生的知识可以装满一个2T(2048G)大小的硬盘。但无论有多少句子需要被书写,对于一个句子来说它最本质的特征是什么呢?毫无疑问,是一个个构成这个句子的单词(对英语来说)或字(对汉语来说)。所以我们可以很傲娇的这样认为,无论人类的知识有多么浩繁,也无论人类的科技有多么发达,一本长不过20厘米,宽不过15厘米,厚不过4厘米的新华字典或牛津字典足以表达人类从古至今乃至未来的所有知识,那些知识只不过是字典中字的排列组合罢了!直到这里,我相信相当一部分读者或许在心中已经明白了字典学习的第一个好处——它实质上是对于庞大数据集的一种降维表示。第二,正如同字是句子最质朴的特征一样,字典学习总是尝试学习蕴藏在样本背后最质朴的特征(假如样本最质朴的特征就是样本最好的特征),这两条原因同时也是这两年深度学习之风日盛的情况下字典学习也开始随之升温的原因。题外话:现代神经科学表明,哺乳动物大脑的初级视觉皮层干就事情就是图像的字典表示。
0.1 - 为什么需要稀疏表示?
同样引用这个博客的一段话,我觉得可以很好的解释这个问题。
回答这个问题毫无疑问就是要回答“稀疏字典学习”中稀疏两字的来历。不妨再举一个例子。相信大部分人都有这样一种感觉,当我们在解涉及到新的知识点的数学题时总有一种累心(累脑)的感觉。但是当我们通过艰苦卓绝的训练将新的知识点牢牢掌握时,再解决与这个知识点相关的问题时就不觉得很累了。这是为什么呢?意大利罗马大学的Fabio Babiloni教授曾经做过一项实验,他们让新飞行员驾驶一架飞机并采集了他们驾驶状态下的脑电,同时又让老飞行员驾驶飞机并也采集了他们驾驶状态下的脑电。如下图所示:
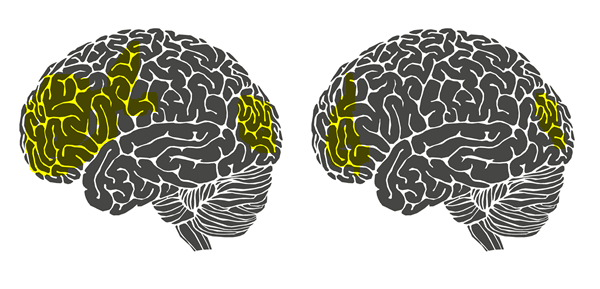
左图是新飞行员(不熟练的飞行员)的大脑。图中黄色的部分,是被认为活跃的脑区。右图是老飞行员(熟练的飞行员)的大脑,黄色区域相比左边的图有明显的减少。换言之,针对某一特定任务(这里是飞行),熟练者的大脑可以调动尽可能少的脑区消耗尽可能少的能量进行同样有效的计算(所以熟悉知识点的你,大脑不会再容易觉得累了),并且由于调动的脑区很少,大脑计算速度也会变快,这就是我们称熟练者为熟练者的原理所在。站在我们所要理解的稀疏字典学习的角度上来讲就是大脑学会了知识的稀疏表示。
稀疏表示的本质:用尽可能少的资源表示尽可能多的知识,这种表示还能带来一个附加的好处,即计算速度快。
1 - 建模
- 将学习对象用$mathbf{Y}$表示,其维度为$M imes N$,$M$表示样本数,$N$表示样本属性个数
- 字典矩阵用$mathbf{D}$表示,其维度为$M imes K$
- 查询矩阵(稀疏矩阵)用$mathbf{X}$表示,其维度为$K imes N$
其中$mathbf{Y}$是已知的,现在需要用$mathbf{D}$和$mathbf{X}$来近似学习对象$mathbf{Y}$。直观地描述即是,现存在知识$mathbf{Y}$,要直接从存在知识中查询开销太大($m$和$n$可能太大),那么可以近似成给定一个查询矩阵$mathbf{X}$和对应的字典$mathbf{D}$,能够使得查询出来的知识和存在的知识差不多就满足要求,并且其中查询矩阵越简单越好(越稀疏越好)。总的来说,即是用两个简单的矩阵来表示一个复杂的矩阵的过程。
将上述问题抽象成优化问题并用数学语言描述如下,
$$min_{mathbf{D},mathbf{X}}left |mathbf{Y}-mathbf{D}mathbf{X} ight |^2_F, s.t. forall i,left |x_i ight |_0leq T_0, $$
或者,也可以描述为如下,
$$minsum_{i}left |x_i ight |_0, s.t.min_{mathbf{D},mathbf{X}}left |mathbf{Y}-mathbf{D}mathbf{X} ight |^2_Fleq T_1, $$
注意到,$left | x_i ight | _0$为零阶范数,但在求解过程中为了方便常常用一阶范数代替。
2 - 求解
用拉格朗日乘子法可以将上述约束问题转化为如下无约束问题,
$$min_{mathbf{D},mathbf{X}}left |mathbf{Y}-mathbf{D}mathbf{X} ight |^2_F+lambdaleft |x_i ight |_1,$$
注意到,这里有两个需要优化的变量$mathbf{X}$和$mathbf{D}$,可以交替的固定一个变量优化另一个变量。
2.0 - 更新$mathbf{D}$
假设$mathbf{X}$已知,记$mathbf{d}_k$为字典矩阵$mathbf{D}$的第$k$列向量,$mathbf{x}^k_T$为查询矩阵$mathbf{X}$的第$k$行向量,那么有如下推导,
$$left |mathbf{Y}-mathbf{D}mathbf{X} ight |^2_F=left |mathbf{Y}-sum_{j=1}^{K}mathbf{d}_jmathbf{x}_T^j ight |^2_F=left |left (mathbf{Y}-sum_{j eq 1}mathbf{d}_jmathbf{x}_T^j ight )-mathbf{d}_kmathbf{x}_T^k ight |^2_F=left | mathbf{E_k}-mathbf{d}_kmathbf{x}_T^k ight |^2_F, $$
其中,$mathbf{E_k}=mathbf{Y}-sum_{j eq 1}mathbf{d}_jmathbf{x}_T^j$,因此现在的优化目标为,
$$min_{mathbf{d}_k,mathbf{x}_T^k}left | mathbf{E_k}-mathbf{d}_kmathbf{x}_T^k ight |^2_F,$$
注意到,这里在优化求解前应该做进一步的过滤,目的是把$mathbf{x}_T^k$中已经为$0$的对应位置都过滤掉,而后再对非$0$的位置求最优化问题(这里的目的是要保证$mathbf{x}_T^k$的稀疏性,如果不过滤掉已经为$0$的位置,虽然也能求解出目标,但无法保证最后的$mathbf{X}$稀疏),过滤过程可以由下图过程直观描述,假设现在求解的是$k=0$(其中的数值均为随机化赋值,不代表什么意义),红色实线框代表当前所求对应的$mathbf{x}_T^k$,红色虚线框代表需要删除的列,过滤后如右侧所示。

因此,将上述最优化问题过滤成如下形式,
$$min_{mathbf{d}_k,mathbf{x}_T^{'k}}left | mathbf{E^{'}_k}-mathbf{d}_kmathbf{x}_T^{'k} ight |^2_F,$$
优化上述问题,可以将$mathbf{E_k^{'}}$做奇异值分解(SVD),记最大的奇异值为$sigma_{max}$,最大奇异值对应的左奇异矩阵$mathbf{U}$的列向量为$mathbf{u}_{max}$,对应的右奇异矩阵$mathbf{V}$的行向量为$mathbf{v}_{max}$,则令$mathbf{d}_k=mathbf{u}_{max}$,$mathbf{x}_T^{'k}=sigma_{max}mathbf{v}_{max}$,再更新到原来的$mathbf{x}_T^k$。(如果求得的奇异值矩阵的奇异值是从大到小排列,那么上述$max=1$,可以替换表示为$mathbf{x}_T^{'k}=Sigmaleft (1,1 ight )V(cdot,1)^T$)。(我觉得上述过程可以这样理解,奇异值分解出来的最大奇异值对应原矩阵最有代表性的特征,删除这个特征可以使得剩下的整体最小,因此选取的是最大奇异值给对应的$mathbf{x}$赋值。)
2.1 - 更新$mathbf{X}$
假设$mathbf{D}$固定之后,可以看作是一个监督问题,因此可以用Lasso或者OMP等算法更新(但需要保证$mathbf{X}$的稀疏性)。
3 - 算法(K-SVD)
- Step 1:初始化。可以从$mathbf{Y}$中随机选取$K$个列向量或者取$mathbf{Y}$的左奇异矩阵的前$K$个列向量初始化$mathbf{D}^{(0)}$
- Step 2:稀疏编码。利用更上一步的字典矩阵$mathbf{D}^{(j)}$来获得新的$mathbf{X}^{(j)}$
- Step 3:计算精度,若精度达到要求,转Step 5,否则转Step 4
- Step 4:逐列更新字典矩阵$mathbf{D}^{(j)}$(如2.0节所讲)
- Step 5:学习完成
这里选取了K分别等于20、50、100、300进行字典学习,获得结果如下图所示,python代码可见于我的github。

4 - 参考资料
https://blog.csdn.net/abc13526222160/article/details/87936459
https://www.cnblogs.com/endlesscoding/p/10090866.html
https://github.com/Chet1996/Notebooks/tree/master/Dictionary%20Learning