0 - 思路
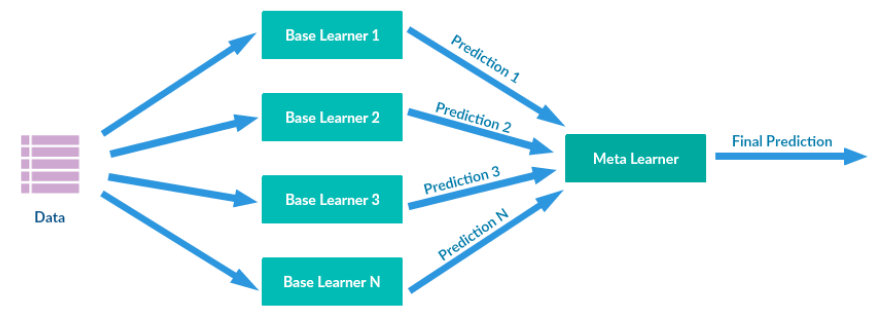
Stacking是许多集成方法的综合。其主要思路如下图所示,通过训练数据训练多个base learners(the first-level learners),这些learners的输出作为下一阶段meta-learners(the second-level learners)的输入,最终预测由meta-learners预测结果得到。
1 - 算法
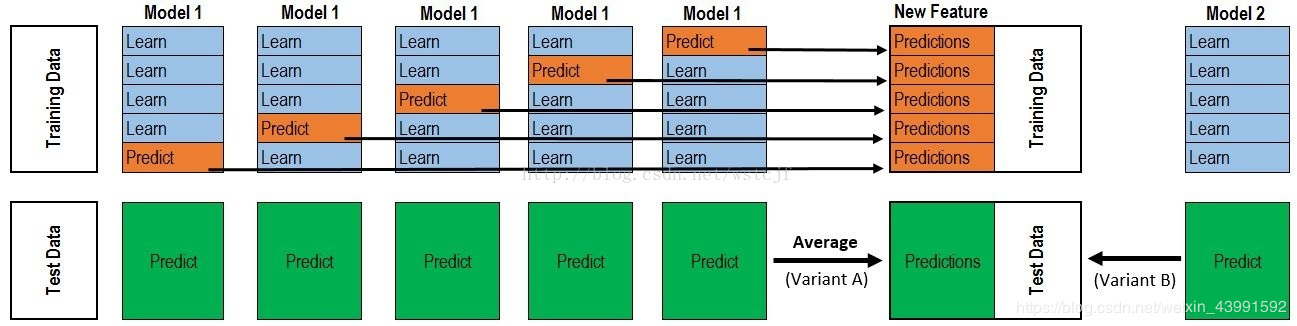
具体地算法如下图所示(图片引自博客)。在第一阶段,采用$K$折交叉验证,首先将训练数据$X_{n imes m}$和对应标签$y_{n}$分成$K$份,训练$K$个base-learners,对于第$i$($i=1,cdots,K$)个base-learner,将第$i$份数据作为验证集,其余$(K-1)$份数据作为训练集进行训练。而后,将第$i$个base-learners对于各自验证集的预测结果$y_{n_i}^{(i)}$(如图中"Predict"橘红色所示)组合起来,即得到和训练数据规模一样的预测结果$y_{n}^{stage1}$(如图中"Predictions"橘红色所示)。将这个第一阶段的预测结果$y_{n}^{stage1}$以及对应的标签$y_{n}$作为第二阶段的meta-learners的训练数据进行训练即可。
在测试过程中,假设对于测试数据$X_{n imes m}^{test}$,经过$K$个base-learners进行预测得到第一阶段预测结果$y_{n imes K}^{stage1}$,而后可以通过硬投票或者软投票或者其他处理方法得到第一阶段的综合预测结果$y_{n}^{stage1}$,再通过meta-learners预测最终的结果$y_{n}^{stage2}$。
注意到,Stacking可以无限叠加下去,也就是stage可以从2开始一直叠加,但实际运用中,一般选取stage为2或者3,因为太多stage对于精度的提高微乎其微甚至没有而计算量却需要大量增加。
2 - 参考资料
https://blog.csdn.net/weixin_43991592/article/details/89962511