我实在是太弱了,为了图省事,就一直用着STL里的 priority_queue 这个优先队列代替堆使用,(*^▽^*)一直用着挺舒服的——
直到我遇见了专门考堆的题,然后发现连题解都看不懂QAQ
我只好到网上去找一找关于堆的讲解,万幸还是有很多对蒟蒻友好的博客,仔细看了看,发现还是很简单的( ̄▽ ̄)~*。
什么是堆?(´`;)?
这个问题一直让我很困扰,因为我最先接触到的堆不是数据结构的堆,而是随机存取存储器(RAM)里面一个区域,堆栈QAQ
后来我才明白这里说的堆,其实是一个数据结构QAQ
它通常是一个可以被看做一棵完全二叉树的数组对象,说白了就是用数组构造的完全二叉树。ヽ(´ー`)ノ
可它是怎么用数组构建一颗完全二叉树的呢?画个图吧来看一下!(图中的标号为结点的序号)

你或许可以轻易的发现(不过别人不告诉我我还真没发现ヽ(#`Д´)ノ)这些结点序号直接有一些关系:
①左子结点的序号是父节点的序号*2
②右子结点的序号是父节点的序号*2+1
③父亲结点的序号的任意一个子节点序号 / 2下取整
这样就可以在数组这样的线性结构中找到一个结点的父结点和子结点了。
怎么建堆呢?(´`;)?
光知道堆大概是什么了不顶用,我们还需要知道怎么把数据构建成一个堆。
堆有两种,大根堆、小根堆,两种的区别就是一个根结点所储存的数值在堆中最大,一个是根结点所储存的数值在堆中最小。
接下来我们就用小根堆来举例说明。
push:
无论你要拿堆做什么,你总得先把数据放进堆里(~ ̄▽ ̄)~ 。
向堆中加入数据其实很简单,你只需要知道它的末尾在哪里,就和读入数组一样就行了。
void push( int num )
{
que[++end] = num;
}
我们将下面这组数据读进去吧!
7 1 2 5 3 6 8 4 9
好,现在我们成功的读入了数据(图中数字为结点所储存的数据)
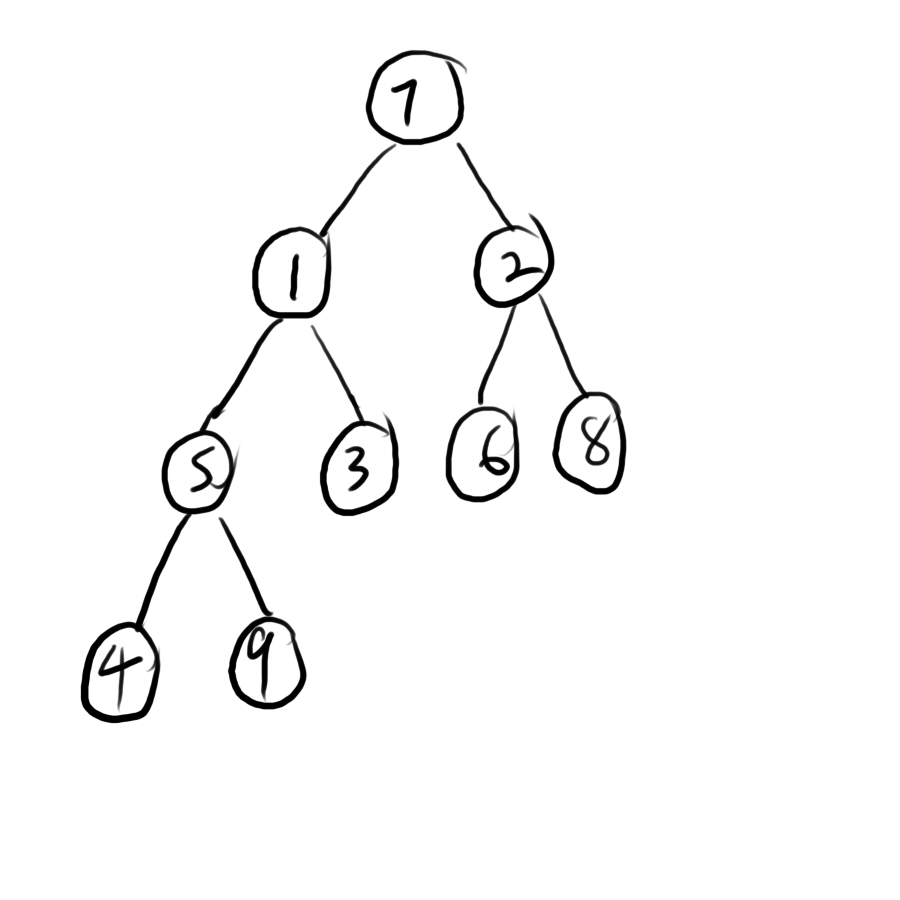
哦!不!这和想象中不一样!Σ(っ°Д°;)っ(虽然有点尬,但是我还是想这么说一下)
很明显,它并没有实现我们需要的功能,我们还缺少一样东西——shift_up(向上维护)
我们每一次插入数据都是往数组尾部插入的,也就是往完全二叉树的最后一层
所以我们想要维护小根堆的性质,就要判断新插入的结点是不是比他的父亲要小,如果比它的父亲小,那就要交换它和它的父亲
什么?Σ(゚д゚lll) 你说它的兄弟怎么办?你想啊,我们每次插入都是往最后插入,那它的兄弟肯定是在它之前插入的,所以已经做过处理了,那它的兄弟就肯定大于他的父亲。
既然都比父亲大了,那咱们肯定不用去管它了。
以下就是向上维护代码:
void shift_up(int now)
{
while( now > 1 )// 还没到堆顶的话就继续
{
int father = now / 2;// 找到父亲
if( que[father] > que[now])// 如果比父亲小
{
swap( que[father] , que[now] );// 交换它和它父亲
now = father;// 移动到父亲的位置继续上述判断
}
else break;// 如果不再比父亲小了,就说明这次插入的影响维护完了
}
}
完整的插入代码:
void push( int num )
{
que[++end] = num;// 插入
shift_up( end );// 向上维护
}
很好(o゚▽゚)o ,我们现在通过不断向堆内插入数据构建好了一个小根堆
pop:
可是,如果我们现在不需要当前的最小值了,我们应该怎么删掉它?
简单粗暴的想,找堆尾的来代替它,然后直接删掉它(因为堆尾好找嘛)φ(>ω<*)
void pop()
{
if(top == end) return;
swap( que[top] , que[end] );
que[end] = 0;
end -= 1;
}
它又不满足小根堆的性质了,这时肯定能想到,我们需要一个东西来维护它——shift_down(向下维护)
当然了,这时候就需要照顾到两个儿子的感受了,你需要在它们当中找一个比较小的来代替这个根的位置,然后继续这样一路维护下去。
void shift_down(int now)
{
while( now <= end )// 到最后了就停止维护
{
int son = que[now * 2] < que[now * 2 + 1] ? now * 2 : now * 2 + 1;
// 找到两个儿子中小的那个
if( que[now] > que[son] )// 如果儿子比爹小
{
swap( que[now] , que[son] );// 交换儿子和爹
now = son;// 移动到儿子的位置继续更新
}
else break;// 如果儿子不再比爹小了,那就说明这次删除造成的影响维护完了
}
}
完整的删除代码:
void pop()
{
if( top == end ) return;// 如果堆里还没有值就不用费劲删了
swap( que[top] , que[end] );// 交换位置
que[end] = 0// 不清零我不舒服
end--;
shift_down( top )// 向下维护
}
对于需要的最值,直接找堆顶就行了。
也就是:
que[top]
完整的手写堆的代码我就不写出来了,把上面的代码组合组合就行了。ヾ(=・ω・=)o
另外,前文中我也提到过了,本人蒟蒻,基本上是用STL的,所以上的代码如果出锅了在下面留言就可以了,请各位大佬轻喷,谢谢您的理解。O(∩_∩)O
φ(>ω<*) CSP ( NOIP ) RP++
