高博SLAM基础课第五讲——PnP非线性优化

这一题很重要

#include <Eigen/Core>
#include <Eigen/Dense>

using namespace Eigen;

#include <vector>
#include <fstream>
#include <iostream>
#include <iomanip>
#include "sophus/se3.h"

using namespace std;

typedef vector<Vector3d, Eigen::aligned_allocator<Vector3d>> VecVector3d;
typedef vector<Vector2d, Eigen::aligned_allocator<Vector3d>> VecVector2d;
typedef Matrix<double, 6, 1> Vector6d;

string p3d_file = "p3d.txt";
string p2d_file = "p2d.txt";

int main(int argc, char **argv) {

    VecVector2d p2d;
    VecVector3d p3d;
    Matrix3d K;
    double fx = 520.9, fy = 521.0, cx = 325.1, cy = 249.7;
    K << fx, 0, cx, 0, fy, cy, 0, 0, 1;

    // load points in to p3d and p2d 
    // START YOUR CODE HERE
    ifstream f3d(p3d_file);
    ifstream f2d(p2d_file);
    double point_3d[3];
    while(!f3d.eof()){
        for(int i=0;i<3;i++)f3d>>point_3d[i];
        p3d.push_back(Vector3d(point_3d[0],point_3d[1],point_3d[2]));
    }
    double point_2d[2];
    while(!f2d.eof()){
        for(int i=0;i<2;i++)f2d>>point_2d[i];
        p2d.push_back(Vector2d(point_2d[0],point_2d[1]));
    }
    // END YOUR CODE HERE
    assert(p3d.size() == p2d.size());
    int iterations = 100;
    double cost = 0, lastCost = 0;
    int nPoints = p3d.size();
    cout << "points: " << nPoints << endl;

    Sophus::SE3 T_esti; // estimated pose

    for (int iter = 0; iter < iterations; iter++) {

        Matrix<double, 6, 6> H = Matrix<double, 6, 6>::Zero();
        Vector6d b = Vector6d::Zero();

        cost = 0;
        // compute cost
        for (int i = 0; i < nPoints; i++) {
            // compute cost for p3d[I] and p2d[I]
            // START YOUR CODE HERE 

            Vector3d P_ = T_esti * Vector3d(p3d[i][0], p3d[i][1], p3d[i][2]);
            double x = P_[0];
            double y = P_[1];
            double z = P_[2];
            double z2 = z * z;
            double x2 = x * x;
            double y2 = y * y;
            Vector3d u = K * P_;
            u = u / u[2];

            Vector2d e(p2d[i][0] - u[0], p2d[i][1] - u[1]);
            cost += e.squaredNorm() / 2;
//        // END YOUR CODE HERE
//
//        // compute jacobian
            Matrix<double, 2, 6> J;
//            // START YOUR CODE HERE

            J(0,0)=fx/z;
            J(0,1)=0;
            J(0,2)=-fx*x/z2;
            J(0,3)=-fx*x*y/z2;
            J(0,4)=fx+fx*x2/z2;
            J(0,5)=-fx*y/z;

            J(1,0)=0;
            J(1,1)=fy/z;
            J(1,2)=-fy*y/z2;
            J(1,3)=-fy-fy*y2/z2;
            J(1,4)=fy*x*y/z2;
            J(1,5)=fy*x/z;
            J=-J;//注意这里1
// END YOUR CODE HERE

            H += J.transpose() * J;
            b += -J.transpose() * e;
        }

    // solve dx 
        Vector6d dx;

        // START YOUR CODE HERE 
            dx=H.ldlt().solve(b);
        // END YOUR CODE HERE

        if (isnan(dx[0])) {
            //cout << "result is nan!" << endl;
            break;
        }

       if (iter > 0 && cost >= lastCost) {
            // cost increase, update is not good
            //cout << "break!!!!"<<"cost: " << cost << ", last cost: " << lastCost << endl;
            break;
        }

        // update your estimation
        // START YOUR CODE HERE 
        T_esti = Sophus::SE3::exp(dx)*T_esti;
        // END YOUR CODE HERE
        
        lastCost = cost;
        //cout << "iteration " << iter << " cost=" << cout.precision(12) << cost << endl;
    }
    clock_t end=clock();


    cout << "estimated pose: 
" << T_esti.matrix() << endl<<"Time use: "<<(end-start)*1000/CLOCKS_PER_SEC<<"ms"<<endl;
    return 0;
}

 注意点：

　　1. 首先读取文件还是使用ifstream方式使用>>操作符输入到数组里

　　2. 各矩阵规模：H 6*6 b 6*1 e 3*1

　　3. 优化问题的策略：

　　　　根据之前李代数一讲的推导，在扰动模型中有以下两式：

　　　　SO3

　　　　 

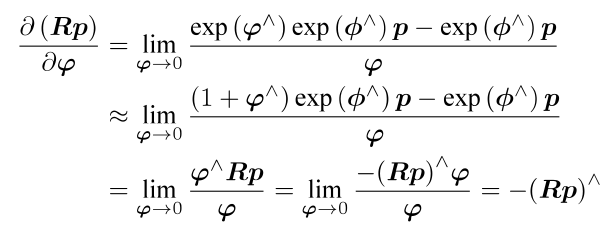
　　　　SE3

　　　　

　　　　

　　　　在本题中的PnP问题使用BA法求解时，待求解量为T，或者说T对应的李代数，每次需要求解的是该李代数相对于误差项定义的导数

　　　　（常规SLAM中是用基础少点的方法如P3P，EPnP等方法解出粗略位姿以方便进行优化，再使用BA整体优化以便快速收敛）

　　　　该优化问题定义为：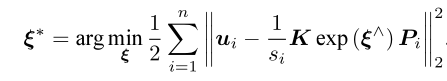

　　　　后续推导：

　　　　

　　　　

　　　　代码中使用的即为7.45式，注意的是矩阵外的负号是由于误差项形式表示为观测值减预测值

　　　　另外，非线性优化求解的几类方法，都是对δx求导数，所以此处的扰动模型对δξ求导正好吻合，并且扰动模型比起求导模型形式更简单。

　　　　注意由于扰动偏导的形式为

　　　　在解出扰动量后，对T进行更新是使用的李代数左乘   T_esti = Sophus::SE3::exp(dx)*T_esti;

　　　　后面的优化模型以该题方法为基础，不过大部分不用手动求解高斯牛顿，皆为调用g2o或者ceres来构造优化项，需要提升性能时需要手动求导数，所以对上方原理需要有较熟练的掌握，也需要对基础的几何模型能够做到手写。

　　　　opencv关于空间问题的文档把几何模型阐述得很清楚，可以作为以后的参考。

　　　　https://docs.opencv.org/3.0-beta/modules/calib3d/doc/camera_calibration_and_3d_reconstruction.html