CodeForces 292D. Connected Components

题目链接

https://codeforces.com/contest/292/problem/D

题面

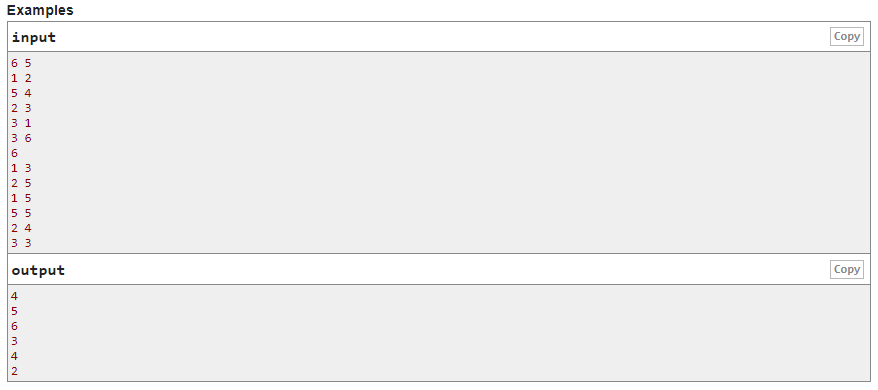
题意

给定 (N)个点，(M)条边的图，(Q)个问题。对于每个问题，给出(l)，(r)，问删去编号在l到r的这些边后有多少个连通块。

思路

令并查集(L)维护边关系的前缀，并查集(R)维护边关系的后缀，那么删除掉([l, r])区间的边，剩下的边关系就是(L[l - 1]) 和 (R[r + 1])部分。
很明显并查集每一次合并都会减少一个连通块，因此再合并的时候统计下次数即可。

AC代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 2e4 + 50;
struct DSU
{
    int far[600], num;
    void init(int n){
        num = 0;
        for(int i = 0; i <= n;i++) far[i] = i;
    }
    int find(int x){
        if(far[x] == x) return x;
        else return far[x] = find(far[x]);
    }
    void unite(int x, int y){
        x = find(x);
        y = find(y);
        if(x == y) return ;
        num++;far[x] = y;
    }
} L[maxn], R[maxn];
int a[maxn], b[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    int n, m;
    cin >> n >> m;
    L[0].init(n);
    R[m + 1].init(n);
    for(int i = 1;i <= m;i++) cin >> a[i] >> b[i];
    for(int i = 1;i <= m;i++){
        L[i] = L[i - 1];
        L[i].unite(a[i], b[i]);
    }
    for(int i = m;i >= 1;i--){
        R[i] = R[i + 1];
        R[i].unite(a[i], b[i]);
    }
    int q;
    cin >> q;
    while(q--)
    {
        int l, r;
        cin >> l >> r;
        DSU t = L[l - 1];
        for(int i = 1;i <= n;i++){
            t.unite(i, R[r + 1].find(i));
        }
        cout << n - t.num << endl;
    }
    return 0;
}