这三道题一定来自USACO,因为USACO就乐意出奶牛的题。
T1 奶牛晒衣服
【问题描述】
在熊大妈英明的带领下,时针和他的同伴生下了许多牛宝宝。熊大妈决定给每个宝宝都穿上可爱的婴儿装。于是,为牛宝宝洗晒衣服就成了很不爽的事情。
圣人王担负起了这个重任。洗完衣服后,你就要弄干衣服。衣服在自然条件下用 1 的时间可以晒干 A 点湿度。抠门的熊大妈买了 1 台烘衣机。使用烘衣机可以让你用 1 的时间使 1件衣服除开自然晒干的 A 点湿度外,还可烘干 B 点湿度,但在 1 的时间内只能对 1 件衣服使用。
N 件的衣服因为种种原因而不一样湿,现在告诉你每件衣服的湿度,要你求出弄干所有衣服的最少时间(湿度为 0 为干)。
【输入格式】
第一行 N , A , B ,接下来N行,每行一个数,表示衣服的湿度(1<= 湿度,A,B<=500000,1<=N<=500000)。
【输出格式】
一行,最少时间。
【输入样例】
Dry.in
3 2 1
1
2
3
【输出样例】
Dry.out
1
【样例解析】
第 1 个时间内,用机器处理第 3 件衣服,此外,所有衣服自然晒干 2。花费 1 时间全部弄干。
我的方法:
通过观察样例和题面不难发现,这是一道贪心题。我们只要想出正确的贪心策略,再模拟一下就可以了。
可行的贪心策略是:每次取湿度最大的衣服用烘干机晾干,直到所有衣服被晾干。
注意,不要每次都sort一遍,会浪费时间,要用优先队列。因为sort是将整个序列排一遍序,在algorithm头文件中,他的时间复杂度为稳定的O(nlogn),而在优先队列中,插入一个元素并把它排好序的时间复杂度的时间为O(logn),所以快很多。
另一种方法
设a[i]为第i件衣服的湿度,当前答案范围是[L,R]。(一开始答案范围是[1,500000])
先二分一个答案ans,然后枚举每件衣服,若a[i]<=ans*A,则表示第i件衣服可以自然晒干,否则表示需要用(a[i]-ans*A)/B(取上整)个单位时间的烘衣机,我们用time累计烘衣机所用的时间。
若最后time<=ans,则表示该答案可行,更新答案,并继续在[L,ans-1]内进行二分答案。
若最后time>ans,则表示该答案不行,继续在[ans+1,R]内进行二分答案。
直到L>R停止。
我的代码:
//Powered by Dev C++ 2018/3/10 08:21 #include<cstdio> #include<algorithm> #include<queue> using namespace std; int k,a,b,c,n; int flag=0; int time=0; int standard; int main() { priority_queue <int> gar; // freopen("dry.in","r",stdin); // freopen("dry.out","w",stdout); scanf("%d%d%d",&n,&a,&b); c = a + b; for(int i=1;i<=n;i++) { scanf("%d",&k); gar.push(k); } while(!gar.empty()) { k = gar.top(); if(k <= standard) break; gar.pop(); k -= b; standard += a; gar.push(k); time++; } printf("%d",time); return 0; }
T2 奶牛排队
【问题描述】
奶牛在熊大妈的带领下排成了一条直队。
显然,不同的奶牛身高不一定相同……
现在,奶牛们想知道,如果找出一些连续的奶牛,要求最左边的奶牛 A 是最矮的,最右边的 B 是最高的,且 B 高于 A 奶牛,且中间如果存在奶牛,则身高不能和 A、B 奶牛相同,问这样的一些奶牛最多会有多少头。
从左到右给出奶牛的身高,请告诉它们符合条件的最多的奶牛数(答案可能是零、二,但不会是一)。
【输入格式】
第一行一个数 N(2<=N<=100000),表示奶牛的头数。
接 下 来 N 个 数 ,每 行 一 个数 , 从 上 到下 表 示 从左 到 右 奶牛 的 身 高 (1<=身高<=maxlongint)。
【输出格式】
一行,表示最多奶牛数。
【输入样例】
Tahort.in
5
1
2
3
4
1
【输出样例】
Tahort.out
4
【样例解析】
取第 1 头到第 4 头奶牛,满足条件且为最多。
题解方法:
题外话:这道题貌似正解是单调栈……只是不知道怎么写,反正Drug是按这个方法讲给我的,但是我没听懂,不过下面的题解很易懂。
对于奶牛的高度序列从L到R,我们可以找出序列中最小高度的奶牛编号min(若有多个,取编号大的)和最大高度的奶牛编号max(若有多个,取编号小的)。那么我们最终的答案序列一定不会跨过这两个奶牛,否则就不是可行序列了。所以整个序列被我们分成了三个部分。
若min<max,则从min到max就是一个可行的序列,用(max-min+1)更新答案,并将[L,min-1]与[max+1,R]分别递归求解。如下图:
若min>max,则将[L,max],[max+1,min-1],[min,R]三部分分别进行递归求解。如下图:
那么现在的问题就是如何尽量快地找出一段序列的最小值与最大值,这是个经典的RMQ问题,使用ST算法。
用f[i][j]表示从i开始长度为2j的一段中的最小值,那么:
f[i][0] = a[i](a[i]表示原序列)
f[i][j] = min{f[i][j-1], f[i+2j-1][j-1]}
用动规便可求出f[i][j]。那么当我们要求[L,R]段的最小值时,就直接可以算出为:
min{f[L][Len], f[R-2Len+1][Len]}(其中Len=trunc(log2(R-L+1)))
f[i][j]的状态量为O(nlog2n),所以我们预处理f[i][j]的时间复杂度为O(nlog2n)。求一段中的最小值时我们就只需要O(1)的时间便可以算出。递归求序列最多有n层,所以总时间复杂度为O(nlog2n+n)。
参考代码:
//Powered by Dev C++ 2018/3/10 09:11 #include<cstdio> #include<algorithm> typedef long long ll; using namespace std; ll a[100000],b[5000000],c[5000000]; ll n,i,maximum; ll bub(ll k,ll l,ll r) { ll o,q,w; o = (l + r) / 2; if (l == r) b[k] = l; else { q = bub(k*2,l,o); w = bub(k*2+1,o+1,r); if(a[q] > a[w]) b[k] = q; else b[k] = w; } return b[k]; } ll bus(ll k,ll l,ll r) { ll o,q,w; o = (l + r) / 2; if (l == r) c[k] = l; else { q = bus(k*2,l,o); w = bus(k*2+1,o+1,r); if(a[q] < a[w]) c[k] = q; else c[k] = w; } return c[k]; } ll fb(ll k,ll l,ll r,ll x,ll y) { ll o,q,w; o = (l + r) / 2; if(x <= b[k] && y >= b[k]) return b[k]; else { if(y <= o) return fb(k*2,l,o,x,y); else if(x > o) return fb(k*2+1,o+1,r,x,y); else { q = fb(k*2,l,o,x,o); w = fb(k*2+1,o+1,r,o+1,y); if(a[q] > a[w]) return q; else return w; } } } ll fs(ll k,ll l,ll r,ll x,ll y) { ll o,q,w; o = (l + r) / 2; if(x <= c[k] && y >= c[k]) return c[k]; else { if(y <= o) return fs(k*2,l,o,x,y); else if(x > o) return fs(k*2+1,o+1,r,x,y); else { q = fs(k*2,l,o,x,o); w = fs(k*2+1,o+1,r,o+1,y); if(a[q] < a[w]) return q; else return w; } } } void work(ll l,ll r) { ll x,y; if(l >= r) return; x = fs(1,1,n,l,r); y = fb(1,1,n,l,r); if(y > x) { if(y-x > maximum) maximum = y - x; if(x-l > 1 + maximum) work(l,x-1); if(r-y > 1 + maximum) work(y+1,r); } else if(y < x) { if(y-1 > maximum) work(l,y); if(x-y > maximum + 2) work(y+1,x-1); if(r-x > maximum) work(x,r); } } int main() { // freopen("tahort.in","r",stdin); // freopen("tahort.out","w",stdout); scanf("%lld",&n); maximum = 1; for(i=1;i<=n;i++) { scanf("%lld",&a[i]); } bub(1,1,n); bus(1,1,n); if(n > 1) work(1,n); printf("%lld",maximum+1); return 0; }
T3 圆圈舞蹈
【问题描述】
熊大妈的奶牛在时针的带领下,围成了一个圈跳舞。由于没有严格的教育,奶牛们之间的间隔不一致。奶牛想知道两只最远的奶牛到底隔了多远。奶牛 A 到 B 的距离为 A 顺时针走和逆时针走,到达 B 的较短路程。告诉你相邻个奶牛间的距离,请你告诉奶牛两只最远的奶牛到底隔了多远。
【输入格式】
第一行一个整数 N,表示有 N 只奶牛。(2<=N<=100000)
接下来 2~N+1 行,第 I 行有一个数,表示第 I-1 头奶牛顺时针到第 I 头奶牛的距离。(1<= 距离<=maxlongint,距离和<=maxlongint)
第 N+1 行的数表示第 N 头奶牛顺时针到第 1 头奶牛的距离
【输出格式】
一行,表示最大距离。
【输入样例】
Circle.in
5
1
2
3
4
5
【输出样例】
Circle.out
7
解析:
这道题需要算法优化。
最笨的方法:多源最短路Floyd,或者从每头牛开始枚举与其他牛的距离,再枚举找到最大距离。时间复杂度是o(n^3),显然不合适。然而我过了四个点(划死。
正确解法:其实我们并不需要知道所有奶牛之间的距离,我们只需要知道对于每头奶牛,离它最远的奶牛的距离是多少。所以首先我们枚举一头奶牛,然后对于这头奶牛求一个最远的奶牛即可(注意:我们应该需要求出两头最远的奶牛,一头顺时针距离最远的,一头逆时针距离最远的)。
对于枚举的第一头奶牛A,我们沿着圈找到一头离它最远的奶牛B。
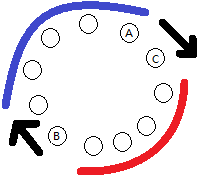
当我们沿着顺时针方向枚举第二头奶牛C时,离C最远的奶牛就不可能是图中红色区域的奶牛了,所以我们只需将B向顺时针方向枚举,当蓝色部分的距离小于红色部分时枚举停止,因为此时蓝色部分的奶牛就不可能是离C最远的奶牛了。
对于这种方法,我们枚举的两个指针分别绕环转了一圈,所以时间复杂度为O(n),可以过题目所给的数据范围了。
参考代码:
//Powered by Dev C++ 2018/3/10 09:43 //Be corrected by 2018/3/10 15:30 //CCCP:Only the dead bear is the good bear. #include<cstdio> #include<algorithm> using namespace std; typedef long long ll; ll shun[100005]; ll nai[100005]; ll ans[100005]; int main() { int n; int flag; ll quan = 0; ll maximum = 0; // freopen("circle.in","r",stdin); // freopen("circle.out","w",stdout); scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%lld",&nai[i]); shun[i] = shun[i-1] + nai[i]; quan += nai[i]; } flag = 1; for(int i=1;i<=n;i++) { for(int j=flag-1;j<=n;j++) { if( min(shun[j+1] - shun[i],quan - (shun[j+1] - shun[i]) ) < min( shun[j] - shun[i],quan - (shun[j] - shun[i]) )) { flag = j; ans[i] = min( shun[j] - shun[i],quan - (shun[j] - shun[i]) ); break; } } } for(int i=1;i<=n;i++) { maximum = max(maximum,ans[i]); } printf("%lld",maximum); return 0; }