---2016/03/10更新-start--
【快速排序性能分析】
参考资料:http://book.51cto.com/art/201108/287089.htm
今天阅读上边的这篇资料,让我对快速排序的性能分析的关键点有了更深入的理解。
前言
我们都知道快速排序的时间复杂度一般为O(N*logN),最坏为O(N*N),那么这两个值是怎么算出来的呢?
每个值的概念:
(1)快速排序的性能取决于递归树的深度。
(2)在最优情况下,递归树深度log2n。(数量级也属于logn)
partition每次均匀划分,如果排序n个关键字,递归树深度为.log2n. + 1(.x.表示对x向下取整),即仅需递归log2n次。
(3)在最坏情况下,递归树深度n。
待排序的序列为正序或者逆序(即有序),每次划分得到的序列只会减少一个记录,另一个为空序列。
此时的递归树,是一棵斜树。
(4)在平均情况下,递归树深度数量级也为logn。
平均情况,也就是说基准元素位于第k(1<=k<=n)个位置。
(5)无论划分好坏,每次划分之后都需要进行n次比较;
结论
现在应该可以理解快排时间复杂度的含义了:
快速排序的时间复杂度 = 递归树的深度*每层比较的次数
所以,当最优情况以及一般情况下,时间复杂度为O(N*logN),最坏情况下,时间复杂度为O(N*N)。
---2016/03/10更新-end--
快速排序的性能分析
快速排序的运行时间与划分是否对称有关,而后者又与选择了那一个元素来进行划分有关。如果划分是对城的,那么快排从渐近意义上来讲,就与合并算法一样快;如果划分是部队称的,那么快排渐近上就和插入算法一样慢。
最坏情况划分
快速排序的最坏情况划分行为发生在划分过程产生的两个区域分别包含n-1个元素和1个0元素的时候。假设算法中的每一次递归调用中都出现了这种不对称的划分。划分的时间代价为Θ(n)。因为对一个大小为0的数组进行递归调用后,返回T(0) = Θ(1),故算法的运行时间可以递归的表示为:
T(n) = T(n-1)+T(0)+Θ(n)=T(n-1)+Θ(n)
从直观上来看,如果将每一层递归的代价加起来,就可以得到一个算术级数,其和值的量级为Θ(n^2)。利用代换法,可以比较直接的证明递归式T(n)=T(n-1)+Θ(n)的解为T=Θ(n^2)。
因此,如果算法的每一层递归上,划分都是最大程度的不对称,那么算法的运行时间就是Θ(n^2)。也就是说,快速排序算法的最坏情况运行时间并不比插入排序更好。此外,当输入数组已经完全有序时,快排的运行时间为Θ(n^2),而在同样情况下,插入排序的运行时间为Θ(n)。
最佳情况划分
在PARTITION可能做的最平衡的划分中,得到的两个子问题的大小都不可能大于n/2,因为其中一个子问题的大小为floor(n/2),另一个子问题的大小为ceil(n/2)-1。在这种情况下,快速排序的运行速度要快很多。这是,表达其运行时间的递归式为
T(n)≤2T(n/2)+Θ(n)
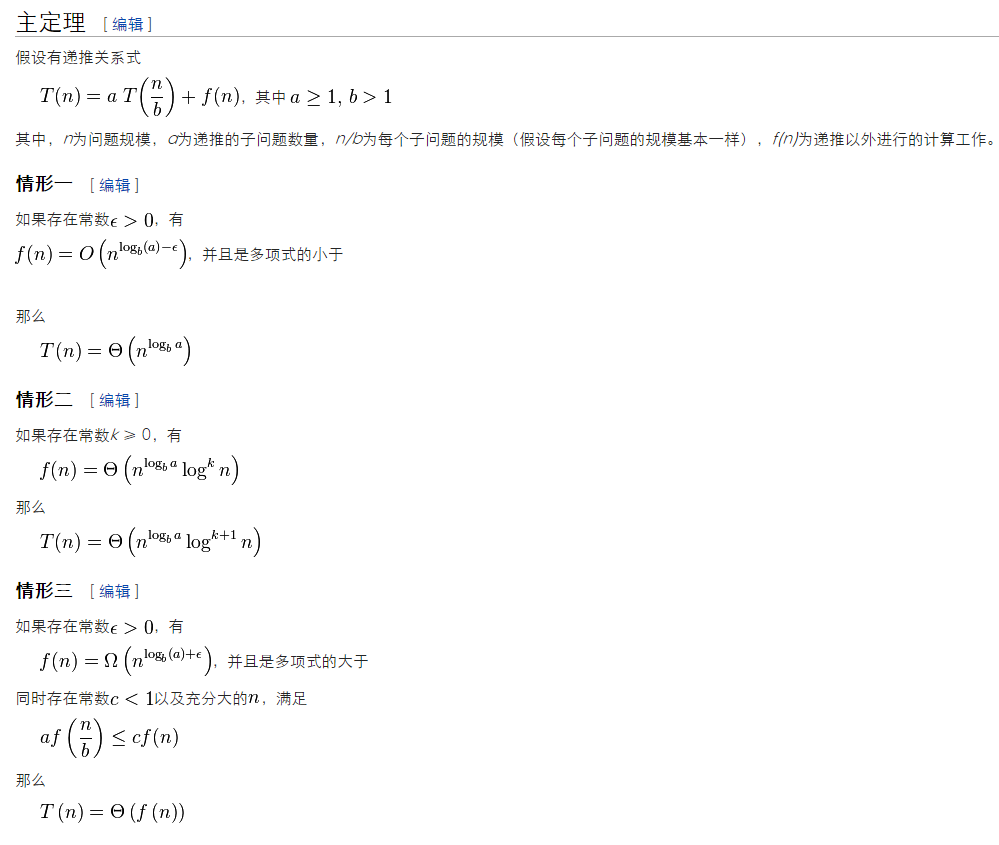
主定理


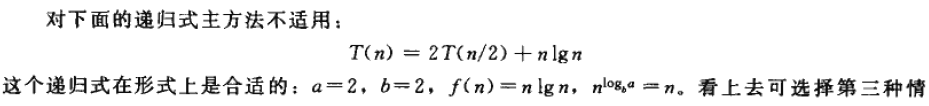

结合维基百科上的解释再来看一下
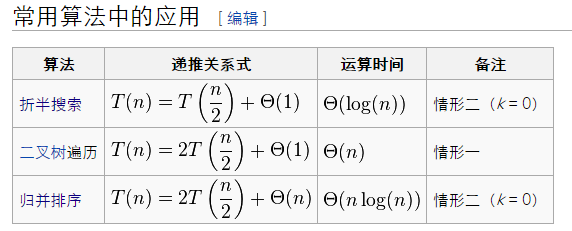
根据主定理的情况2,该递归式的解为T(n)=O(n*lg(n))。由于在每一层递归上,划分的两边都是对称的,因此,从渐近意义上来看,算法运行的就更快了。
平衡的划分
快速排序的平均情况运行时间与其最佳情况运行时间接近,而不是非常接近于其最坏情况运行时间。要理解这一点,就要理解划分的平衡性是如何在刻划运行时间的递归式中反映出来的。
例如,假设划分过程总是产生9:1的划分,乍一看这种划分很不平衡,这时,快速排序运行时间的递归式为:
T(n)≤T(9n/10)+T(n/10)+cn
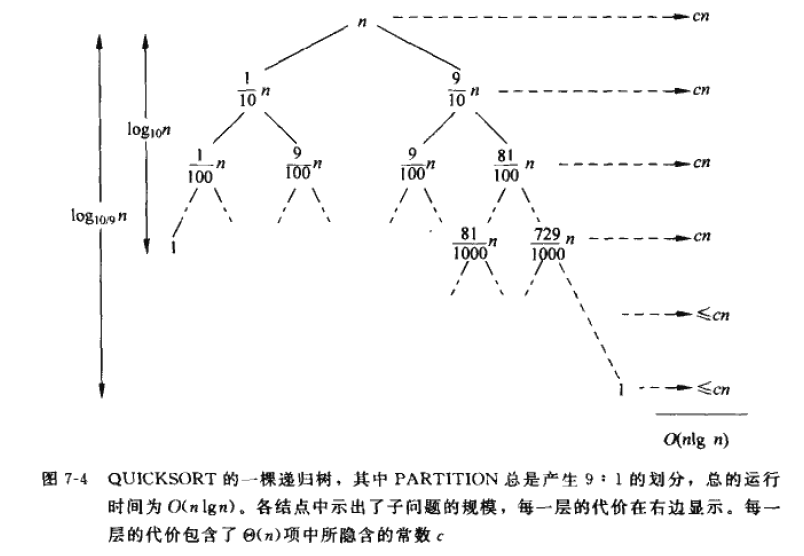
此处,我们显示地写出了Θ(n)项中所隐含的常数c。图7-4示出了与这一递归式对应的递归树。请注意该树每一层的代价都是cn,直到在深度log10n=Θ(lgn)处达到边界条件时为止,在此之下各层的代价至多为cn。递归于深度log10/9n=Θ(lgn)处终止。这样,快速排序的总代价为O(nlgn)。在递归的每一层上是按照9:1的比例进行划分的,直观上看上去好像应该是相当不平衡的,但在这种情况下,快速排序的运行时间为O(nlgn),从渐近意义上来看,这与划分是在正中间进行的效果是一样的。事实上按照99:1划分运行时间也为O(nlgn)。其原因在于,任何一种按照常数比例进行的划分都会产生深度为Θ(lgn)的递归树,其中每一层的代价为O(n),因而,每当按照常数比例进行划分时,总的运行时间都是O(nlgn)。
参考资料:《算法导论》,主定理——维基百科