HDU 6395（矩阵快速幂）

传送门

题面：

Sequence

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 696    Accepted Submission(s): 242

Problem Description

Let us define a sequence as below

⎧⎩⎨⎪⎪⎪⎪⎪⎪F1F2Fn===ABC⋅Fn−2+D⋅Fn−1+⌊Pn⌋
  Your job is simple, for each task, you should output Fn module 109+7.

Input

The first line has only one integer T, indicates the number of tasks.

Then, for the next T lines, each line consists of 6 integers, A , B, C, D, P, n.

1≤T≤200≤A,B,C,D≤1091≤P,n≤109

Sample Input

2 3 3 2 1 3 5 3 2 2 2 1 4

Sample Output

36 24

Source

2018 Multi-University Training Contest 7

题目描述：

    给你一个式子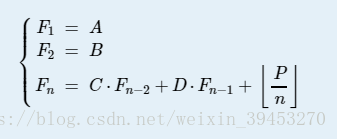，给出你A,B,C,D,P,n，让你求出第n项的式子Fn。（其中ABCDPn均在1e9的范围内）

题目分析：

    题目中给了我们一个递推的式子，让我们求第n项的数，我们分析题目中的数据范围，因为题目中的所有参数均在1e9的级别，因此倘如我们直接递推求解必定超时，因此我们需要用矩阵快速幂(logn)进行优化。

    要用矩阵快速幂求解，首先我们需要讲上面的递推式转化成矩阵转移方程的形式。

    因为第n项中有三个不同的参数，因此我们考虑建立一个3*3的矩阵进行求解。不难求出，矩阵的转移方程形式为：

（验证是否正确就是将等号左边的矩阵相乘后判断是否等于等号右边的式子）。

    很明显，倘若矩阵中没有[0,2]项,的话，我们直接就可以用矩阵快速幂求出第n项。但是因为多出一个需要下取整的数，我们不能直接进行矩阵快速幂求解。

   此时我们需要对进行简单的分析。当我们任取p和n时，我们可以发现，的值的分布是呈一定的规律性的。

    当第i位的值为x时，那么第项也必定为x，且在第i项到第项中的数也必定为x。（证明略）

    因此，根据上诉的性质，我们就可以将矩阵快速幂分段的去进行。若当前的位数仍在p以内，则根据上述性质，我们可以将这一段矩阵的值根据矩阵快速幂求出，然后将矩阵更新后再进行下一段的求解。

    而倘若当前的位数i大于p，则证明i以后的所有项中，矩阵[0,2]已经变为0，因此此时直接对剩下的项进行矩阵快速幂求解即可。

#include <bits/stdc++.h>
#define maxn 100005
using namespace std;
const int mod=1e9+7;
typedef long long ll;
struct Marix{
    ll mo[3][3];
    Marix(){
        memset(mo,0,sizeof(mo));
    }
};
Marix mul(Marix a,Marix b){
    Marix c;
    for(int i=0;i<3;i++){
        for(int j=0;j<3;j++){
            for(int k=0;k<3;k++){
                c.mo[i][j]=(c.mo[i][j]+a.mo[i][k]*b.mo[k][j])%mod;
            }
        }
    }
    return c;
}
Marix powmod(Marix a,ll n){//矩阵快速幂模板
    Marix tmp;
    for(int i=0;i<3;i++){
        tmp.mo[i][i]=1;
    }
    while(n){
        if(n&1) tmp=mul(tmp,a);
        n>>=1;
        a=mul(a,a);
    }
    return tmp;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--){
        ll a,b,c,d,p,n;
        scanf("%lld%lld%lld%lld%lld%lld",&a,&b,&c,&d,&p,&n);
        if(n==1){
            printf("%lld
",a);
            continue;
        }
        if(n==2){
            printf("%lld
",b);
            continue;
        }
        Marix m;
        m.mo[0][0]=d,m.mo[0][1]=c,m.mo[1][0]=1,m.mo[2][2]=1;
        bool vis=0;
        for(ll i=3;i<=n;){
            if(p/i==0){//倘若当前项大于p了，则直接用矩阵快速幂求解剩下的项
                Marix tmp;
                tmp=m;
                tmp=powmod(tmp,n-i+1);
                ll res=(tmp.mo[0][0]*b+tmp.mo[0][1]*a+tmp.mo[0][2])%mod;
                printf("%lld
",res);
                vis=1;
                break;
            }//否则，不断的分段求解矩阵的值，并将矩阵的值进行修改
            ll j=min(n,p/(p/i));
            Marix tmp;
            tmp=m;
            tmp.mo[0][2]=p/i;
            tmp=powmod(tmp,j-i+1);
            ll A=(tmp.mo[1][0]*b+tmp.mo[1][1]*a+tmp.mo[1][2])%mod;
            ll B=(tmp.mo[0][0]*b+tmp.mo[0][1]*a+tmp.mo[0][2])%mod;
            a=A,b=B;
            i=j+1;
        }
        if(!vis) printf("%lld
",b);
    }
    return 0;
}