- 写在开头:
临近毕业准备找工作,而机器学习方法是复习中不可缺少的一个重要部分,所以本篇博文是将之前做过的一个项目里面应用的机器学习方法——朴素贝叶斯方法,重点复习一遍。具体文章如下引用所示。
Zhang S, Chen Z, Gu S, et al. Breast tumor detection in double views mammography based on Simple Bias[C]. Medical Imaging Physics and Engineering (ICMIPE), 2013 IEEE International Conference on. IEEE, 2013: 240-244.
- 文章概述:
背景:乳腺肿块检测对于医生来说是一个很繁杂的工作,如果能利用计算机辅助诊断的方法自动地识别乳腺钼靶X射线中的可疑肿块,并标记出来,可以大大地减少医生的重复性劳动,提高医生的诊断效率。通常医生会利用同侧乳腺的两个视图进行同时比较,增加诊断结果的可靠性,因此我们提出的方法也与此类似,分别对两个视图进行分类,然后再用贝叶斯分类器对单独分类的结果进行综合分类,从而综合双视图的结果来进行判断就可以大大地增加分类精度。
方法:利用朴素贝叶斯方法训练一种能够对乳腺钼靶X射线的同侧乳腺不同视图(MLO视图和CC视图)的图像中的可疑区域进行自动分类,综合两个视图判断其是否存在有肿块。
概述:
1. 预处理双侧视图的图像,包括图像预处理和可疑肿块边缘提取。图像预处理包括中值滤波和对比度增强;边缘提取包括ROI提取、小波变换模极大值法提取边缘、形态学操作和区域增长。
2. 分别提取可疑区域的几何特征和纹理特征,包括5个几何特征:the entropy of standard radius, roundness, roughness, variance of standardized radius, ratio of area;5个基于灰度共生矩阵的5个纹理特征:energy, entropy, inverse difference moment, correlated coefficient, contrast。
3. 将提取的特征输入极限学习机(ELM)中进行学习,并得到两个视图的分类结果。
4. 根据极限学习机对双视图分类的结果再用贝叶斯分类器进行综合分类,提高分类精度。
总体框架图如下所示:
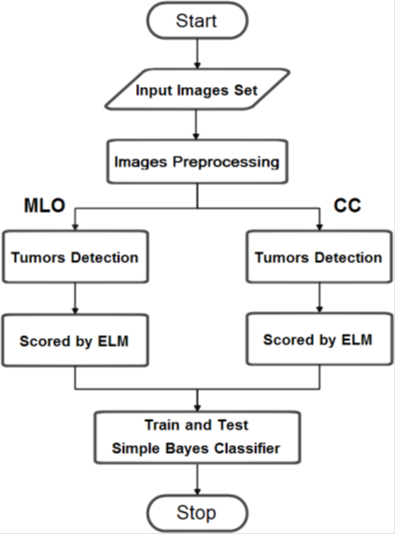
文章贡献点:
1. 利用同侧双视图进行综合分类,模拟医生的诊断过程。
2. 将朴素贝叶斯分类器应用到乳腺肿块的辅助诊断中。
- 朴素贝叶斯概述:
由于博客园中编辑公式不方便,所以以下内容以word截图展现。




- 朴素贝叶斯在乳腺肿块分类上的应用:


- 评价分类器:
真阳(True Positive):TP,真阴(True Negative):TN,假阳(False Positive):FP,假阴(False Negative):FN。
|
指标 |
计算公式 |
|
准确率 |
(TP+TN) / (TP+TN+FP+FN) |
|
敏感性(真阳率,TPR) |
TP / (TP+FN) |
|
特异性(假阳率,FPR) |
TN / (TN+FP) |
|
错误正比率 |
TP / (TP+FP) |
|
错误负比率 |
TN / (TN+FN) |
注:以上指标均为越高越好
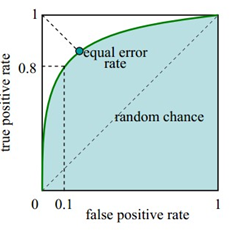
用来评价分类器的ROC(Receiver Operating Characteristic)曲线:一个优良的二分类器应该具有很高的真阳率和很低的假阳率。那么只需要只需要真阳性率和假阳性率就可以画ROC曲线。ROC空间将FPR定义为x轴,TPR定义为y轴。因此曲线与横轴所围区域面积越大,则认为分类的效果越好。