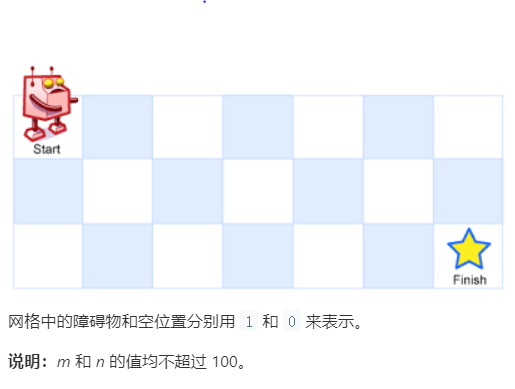
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
dp[m][n] 初始化:
62题无障碍物: dp = [[1]*n] + [[1] + [0]*(n-1) for _ in range(m-1)]
63题有障碍物: 初始化两条边:如果对应节点有障碍物,或上一个节点为0,本节点为0
dp = [[0]*n for _ in range(m)]
dp[0][0] = 1
for i in range(1,n):
dp[0][i] = 0 if obstacleGrid[0][i] or not dp[0][i-1] else 1
for j in range(1,m):
dp[j][0] = 0 if obstacleGrid[j][0] or not dp[j-1][0] else 1
dp状态转移方程:
62: dp[i][j] = dp[i][j-1] + dp[i-1][j]
63: 根据本节点,左节点,上节点有障碍物来 分别写状态转移方程
for i in range(1,m):
for j in range(1,n):
if obstacleGrid[i][j] : dp[i][j] = 0
elif obstacleGrid[i][j-1] and obstacleGrid[i-1][j]:
dp[i][j] = 0
elif obstacleGrid[i-1][j]:
dp[i][j] =dp[i][j-1]
elif obstacleGrid[i][j-1]:
dp[i][j] = dp[i-1][j]
else:
dp[i][j] = dp[i-1][j] + dp[i][j-1]