1712: [Usaco2007 China]Summing Sums 加密
Time Limit: 5 Sec Memory Limit: 64 MBSubmit: 526 Solved: 205
[Submit][Status][Discuss]
Description
那N只可爱的奶牛刚刚学习了有关密码的许多算法,终于,她们创造出了属于奶牛的加密方法.由于她们并不是经验十足,她们的加密方法非常简单:第i只奶牛掌握着密码的第i个数字,起始的时候是Ci(0≤Ci<90000000).加密的时候,第i只奶牛会计算其他所有奶牛的数字和,并将这个数字和除以98765431取余.在所有奶牛计算完毕之后,每一只奶牛会用自己算得的数字代替原有的数字.也就是说,
.jpg)
这样,她们就完成了一次加密. 在十一月,奶牛们把这个加密法则告诉了驼鹿卡门,卡门惊呆了.之后,在一个浓雾弥漫的平安夜,卡门与奶牛们:“你们的算法十分原始,很容易就被人破解.所以你们要重复这个加密过程T(1≤T≤1414213562)次,才能达到加密效果.” 这回轮到奶牛们惊呆了.很显然,奶牛们特别讨厌做同样的无聊的事情很多次.经过了漫长的争论,卡门和奶牛们终于找到的解决办法:你被刚来加密这些数字.
Input
第1行输入N和T,之后N行每行一个整数表示初始的Ci.
Output
共N行,每行一个整数,表示T次加密之后的Ci.
Sample Input
3 4
1
0
4
INPUT DETAILS:
Three cows, with starting numbers 1, 0, and 4; four repetitions of the
encryption algorithm.
1
0
4
INPUT DETAILS:
Three cows, with starting numbers 1, 0, and 4; four repetitions of the
encryption algorithm.
Sample Output
26
25
29
OUTPUT DETAILS:
The following is a table of the cows' numbers for each turn:
Cows' numbers
Turn Cow1 Cow2 Cow3
0 1 0 4
1 4 5 1
2 6 5 9
3 14 15 11
4 26 25 29
25
29
OUTPUT DETAILS:
The following is a table of the cows' numbers for each turn:
Cows' numbers
Turn Cow1 Cow2 Cow3
0 1 0 4
1 4 5 1
2 6 5 9
3 14 15 11
4 26 25 29
HINT
N<=50000
Source
Analysis
瞬间想到矩阵快速幂
但是令人沮丧的是: n <= 500000
就算时间复杂度压下来了,空间复杂度也会爆的
所以翻了一发题解
发现可以根据单个元素进行构造矩阵
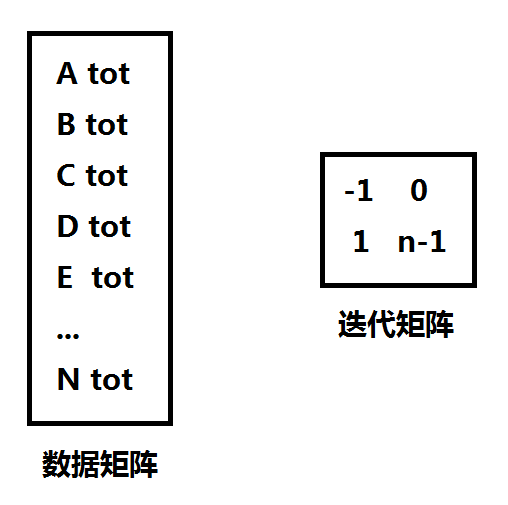
之所以这样是因为经过模拟发现tot有这样的性质
(tot指当前所有数之和)
每次迭代后 tot 为原来的 n-1 倍
其余细节不难思考
Code

1 #include<cstdio> 2 #include<iostream> 3 #define mod 98765431 4 using namespace std; 5 6 long long arr[100000][3],brr[100000][3],n,t,tot; 7 8 struct MAT{ 9 long long mat[10][10]; 10 MAT(){ 11 for(int i = 0;i < 10;i++) 12 for(int j = 0;j < 10;j++) 13 mat[i][j] = 0; 14 } 15 }; 16 17 MAT mul(MAT A,MAT B){ 18 MAT C; 19 for(int i = 1;i <= 2;i++) 20 for(int j = 1;j <= 2;j++) 21 for(int k = 1;k <= 2;k++) 22 C.mat[i][j] = (C.mat[i][j]+A.mat[i][k]*B.mat[k][j])%mod; 23 return C; 24 } 25 26 MAT ksm(MAT A,long long k){ 27 if(k == 1) return A; 28 MAT B = A; k--; 29 while(k){ 30 if(k&1) B = mul(B,A); 31 A = mul(A,A); 32 k >>= 1; 33 }return B; 34 } 35 36 int main(){ 37 scanf("%lld%lld",&n,&t); 38 for(int i = 1;i <= n;i++) 39 scanf("%lld",&arr[i][1]); 40 MAT BUF; 41 BUF.mat[1][1] = -1; 42 BUF.mat[1][2] = 0; 43 BUF.mat[2][1] = 1; 44 BUF.mat[2][2] = n-1; 45 46 BUF = ksm(BUF,t); 47 48 for(int i = 1;i <= n;i++) tot += arr[i][1]; 49 for(int i = 1;i <= n;i++) arr[i][2] = tot%mod; 50 51 for(int i = 1;i <= n;i++) 52 for(int j = 1;j <= 2;j++) 53 for(int k = 1;k <= 2;k++) 54 brr[i][j] = (brr[i][j]+arr[i][k]*BUF.mat[k][j])%mod; 55 56 for(int i = 1;i <= n;i++) 57 printf("%lld ",brr[i][1]); 58 59 return 0; 60 }
