《视觉slam十四讲》之第５讲－单目相机模型

单目相机模型

相机将三维世界中的坐标点（单位为米）映射到二维图像平面（单位为像素）的过程

1.1 针孔相机模型

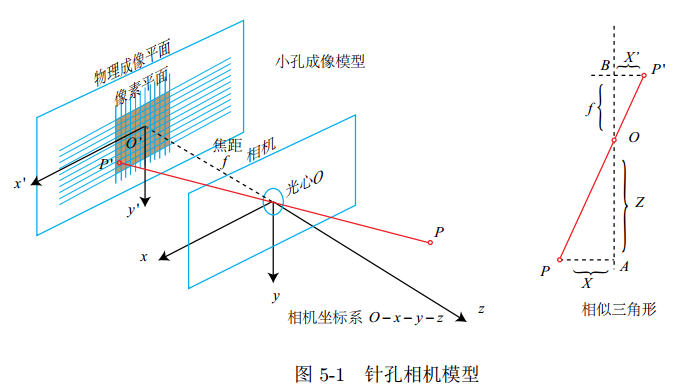
几种坐标系

• 世界坐标系P_w， 单位是m
• 相机坐标系P_c， 单位是m
• 像素坐标系P_uv， 单位是像素

相机坐标系的原点为相机的光心， x轴指向右方， y轴指向下方，z轴指向前方。

像素坐标系的原点为图像的左上角，u轴指向右方， y轴指向下方。

注：opencv中的图像坐标系和这个像素坐标系是一样的。

• 相机坐标系与像素坐标系的转换：

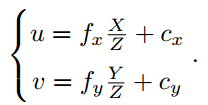
•  针孔相机的观测方程：

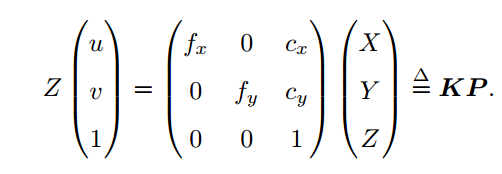
注： 内参数矩阵（ Camera Intrinsics） K

• 世界坐标系与像素坐标系的转换

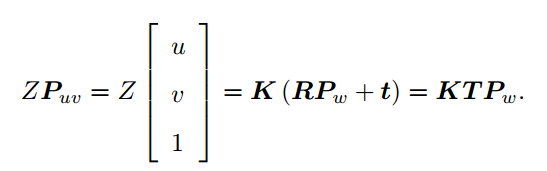
注：其中包含了齐次坐标到非齐次坐标的转换

1.2 畸变模型

由透镜形状引起的畸变称之为径向畸变，分为两大类， 桶形畸变和枕形畸变

• 径向畸变函数矫正公式：

• 切向畸变函数矫正公式：

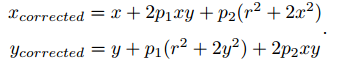
整理可得：

1.3 单目相机成像过程

• 1. 首先，世界坐标系下有一个固定的点 P，世界坐标为 P_w；
• 2. 由于相机在运动，它的运动由 R; t 或变换矩阵 T 2 SE(3) 描述。 P 的相机坐标为：P_c= RP_w + t。
• 3. 这时的 Pc 仍有 X; Y; Z 三个量，把它们投影到归一化平面 Z = 1 上，得到 P 的归一化相机坐标： P_c = [X/Z; Y /Z;1]^T。
• 4. 最后， P 的归一化坐标经过内参后，对应到它的像素坐标： P_uv = KP_c。

世界坐标系->相机坐标系->归一化处理-> 像素坐标系