逻辑回归
线性回归是特征的线性组合来拟合真实标记,逻辑回归是特征的线性组合拟合真实标记的正例的概率的对数几率
一句话总结:逻辑回归假设数据服从伯努利分布,通过极大化似然函数的方法,运用梯度下降来求解参数,来达到将数据二分类的目的。
a.假设有模型P(Y=1|x)=F(x)=1/1+e−θTx,在已知输入x的情况下,判断此输入为1类的概率是多少。
b.而在此概率模型中,若想求得概率P,只有参数θT不知道。
c.如何求得参数θT,就需要估计参数值。参数估计方法则采用在模型已知,参数未知的情况下的极大似然估计。
d.若采用极大似然估计方法来估计参数,那么就需要给出似然函数。在整个模型训练中,似然函数如何表示?问题转化成如何表达极大似然估计函数
逻辑回归,softmax回归,最大熵模型
都属于对数线性模型,逻辑回归和softmax回归基于条件概率模型,N重伯努利分布,最大熵以期望为准,采用线性模型,假设特征之间独立。
逻辑回归:分类是回归问题的一个分类,逻辑回归可以多个角度理解,概率解释和最小对数损失,直接的理解是线性回归离散化,二分类问题。逻辑回归服从伯努利分布,通过极大似然估计,通过梯度下降法,降低损失。
softmax :
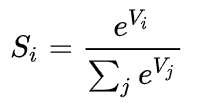
为什么要取指数,第一个原因是要模拟max的行为,所以要让大的更大。第二个原因是需要一个可导的函数。
让大的更大的原因是让错的更错,这样学习效率更高。好比以前考试错了,老师轻轻说了两句,换成softmax两巴掌上去,你说哪个学习效率高?
交叉熵:两个概率分布的距离,或者概率q表达概率p的困难程度,q为预测值;
互信息:两个随机变量相关性的大小,已知一个变量,另一个变量不确定性减少的程度
相对熵(KL散度):同一个随机变量对两个概率分布p(x),q(x)的差异性,用概率q来近似P时造成的信息损失量
JS散度:一种对称的衡量两个分布相似度的度量方式。
GBDT
gbdt通过多轮迭代,每轮迭代产生一个弱分类器,每个分类器在上一轮分类器的残差基础上进行训练。对弱分类器(一般使用cart决策树)的要求一般是足够简单,并且是低方差和高偏差的。因为训练的过程是通过降低偏差来不断提高最终分类器的精度。

参考:mod_ai