题目1 ID121
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易(即买入和卖出一支股票),设计一个算法来计算你所能获取的最大利润。
注意你不能在买入股票前卖出股票。
示例 1:
输入: [7,1,5,3,6,4]输出: 5解释: 在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
示例 2:
输入: [7,6,4,3,1]输出: 0解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
我的解答:
动态规划类题目,做动态规划的题目做的比较少,专门训练一下,动态规划通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。观察题目即可得出动态规划方程(得出动态规划方程其实是最难的一步):
dp[i]=max(dp[i-1],prices[i]-min)
我们使用dp[i]代表当前天数能够拥有的最大利润,而dp[i]又等于前一天能够拥有的最大利润,或者是今天股票价格减去前几天股票最小值的差,这两个中的更大的那一个。最后我们返回dp[pricesSize-1],就是能拥有的最大利润,如果其小于等于0,我们直接返回0
int min(int a,int b){
return a<b?a:b;
}
int max(int a,int b){
return a>b?a:b;
}
int maxProfit(int* prices, int pricesSize){
if(pricesSize==0||pricesSize==1){
return 0;
}
int* dp=(int*)malloc(sizeof(int)*pricesSize);
int minnum=min(prices[0],prices[1]),i;
dp[0]=0;
dp[1]=prices[1]-prices[0];
for(i=2;i<pricesSize;i++){
if(prices[i]<minnum){
minnum=prices[i];
}
dp[i]=max(dp[i-1],prices[i]-minnum);
}
if(dp[pricesSize-1]<=0){
return 0;
}
return dp[pricesSize-1];
}
题目2 ID392

给定一个整数数组 nums,求出数组从索引 i 到 j (i ≤ j) 范围内元素的总和,包含 i, j 两点。
示例:
给定 nums = [-2, 0, 3, -5, 2, -1],求和函数为 sumRange()
sumRange(0, 2) -> 1
sumRange(2, 5) -> -1
sumRange(0, 5) -> -3
说明:
你可以假设数组不可变。
会多次调用 sumRange 方法。
我的解答:
我们可以使用暴力法直接遍历i-->j之间的值,相加之后返回。这里使用动态规划的做法,预处理比较消耗时间,但查询区域和的时候时间复杂度是O(1),使用另一数组,第i位储存前面i位的和,查询区域和时返回sum[j]-sum[i]+nums[i]即可,使用python作答
class NumArray(object):
def __init__(self, nums):
if len(nums)==0:
return
self.nums=nums;
self.sums=[0]*len(nums)
self.sums[0]=nums[0];
for i in range(1,len(nums)):
self.sums[i]=self.sums[i-1]+nums[i]
def sumRange(self, i, j):
return self.sums[j]-self.sums[i]+self.nums[i]
# Your NumArray object will be instantiated and called as such:
# obj = NumArray(nums)
# param_1 = obj.sumRange(i,j)
题目3 ID746

数组的每个索引做为一个阶梯,第 i个阶梯对应着一个非负数的体力花费值 cost[i](索引从0开始)。
每当你爬上一个阶梯你都要花费对应的体力花费值,然后你可以选择继续爬一个阶梯或者爬两个阶梯。
您需要找到达到楼层顶部的最低花费。在开始时,你可以选择从索引为 0 或 1 的元素作为初始阶梯。
示例 1:
输入: cost = [10, 15, 20]
输出: 15
解释: 最低花费是从cost[1]开始,然后走两步即可到阶梯顶,一共花费15。
示例 2:
输入: cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1]
输出: 6
解释: 最低花费方式是从cost[0]开始,逐个经过那些1,跳过cost[3],一共花费6。
注意:
cost 的长度将会在 [2, 1000]。
每一个 cost[i] 将会是一个Integer类型,范围为 [0, 999]。
我的解答:
由题得出动态规划方程,nums[i]=min(nums[i-1]+cost[i],nums[i-2]+cost[i]);因为有这种情况存在1,2,3,100,实际上我们可以跳过100,从3的阶梯上跨两格到终点,所以最后的结果应当是在nums[costSize-1],nums[costSize-2]之间取较小的那一个。
int min(int a,int b){
return a<b?a:b;
}
int minCostClimbingStairs(int* cost, int costSize){
int i;
int* nums=(int*)malloc(sizeof(int)*costSize);
nums[0]=cost[0];
nums[1]=cost[1];
for(i=2;i<costSize;i++){
nums[i]=min(nums[i-1]+cost[i],nums[i-2]+cost[i]);
}
return min(nums[costSize-1],nums[costSize-2]);
}
题目4 ID392

给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
你可以认为 s 和 t 中仅包含英文小写字母。字符串 t 可能会很长(长度 ~= 500,000),而 s 是个短字符串(长度 <=100)。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
示例 1:
s = "abc", t = "ahbgdc"
返回 true.
示例 2:
s = "axc", t = "ahbgdc"
返回 false.
后续挑战 :
如果有大量输入的 S,称作S1, S2, ... , Sk 其中 k >= 10亿,你需要依次检查它们是否为 T 的子序列。在这种情况下,你会怎样改变代码?
我的解答:
很容易会想到遍历数组匹配。
bool isSubsequence(char * s, char * t){
int i,j;
for(i=0,j=0;j<strlen(s)&&i<strlen(t);i++){
if(t[i]==s[j]){
j++;
}
}
if(j==strlen(s)){
return true;
}else{
return false;
}
}
但是使用for循环超时了,改用双指针之后就过了,思路相同,是因为双指针指针指向更快吗?
bool isSubsequence(char * s, char * t){
while(*s&&*t){
if(*s==*t){
s++;
}
t++;
}
if(*s=='�'){
return true;
}
return false;
}
题目5 ID面试题17.16

一个有名的按摩师会收到源源不断的预约请求,每个预约都可以选择接或不接。在每次预约服务之间要有休息时间,因此她不能接受相邻的预约。给定一个预约请求序列,替按摩师找到最优的预约集合(总预约时间最长),返回总的分钟数。
注意:本题相对原题稍作改动
示例 1:
输入: [1,2,3,1]
输出: 4
解释: 选择 1 号预约和 3 号预约,总时长 = 1 + 3 = 4。
示例 2:
输入: [2,7,9,3,1]
输出: 12
解释: 选择 1 号预约、 3 号预约和 5 号预约,总时长 = 2 + 9 + 1 = 12。
示例 3:
输入: [2,1,4,5,3,1,1,3]
输出: 12
解释: 选择 1 号预约、 3 号预约、 5 号预约和 8 号预约,总时长 = 2 + 4 + 3 + 3 = 12。
我的解答:
跟之前的动态规划题目类似,写出动态规划方程之后即可写出代码
int max(int a,int b){
return a>b?a:b;
}
int massage(int* nums, int numsSize){
if(numsSize==0){
return 0;
}
if(numsSize==1){
return nums[0];
}
int* time=(int*)malloc(sizeof(int)*numsSize);
int i;
time[0]=nums[0];
time[1]=max(nums[0],nums[1]);
for(i=2;i<numsSize;i++){
time[i]=max(time[i-2]+nums[i],time[i-1]);
}
return time[numsSize-1];
}
题目6 ID面试题08.01

三步问题。有个小孩正在上楼梯,楼梯有n阶台阶,小孩一次可以上1阶、2阶或3阶。实现一种方法,计算小孩有多少种上楼梯的方式。结果可能很大,你需要对结果模1000000007。
示例1:
输入:n = 3
输出:4
说明: 有四种走法
示例2:
输入:n = 5
输出:13
提示:
n范围在[1, 1000000]之间
我的解答:
之前做过上两个阶梯的动态规划问题,将前几次的上阶梯的走法列出来,找到规律写代码,当n>=3时,动态规划方程为:nums[i]=(nums[i-3]+nums[i-1]+nums[i-2])
int waysToStep(int n){
if(n==0||n==1){
return 1;
}
if(n==2){
return 2;
}
if(n==3){
return 4;
}
long* nums=(long*)malloc(sizeof(long)*(n+1));
int i;
nums[0]=1;
nums[1]=1;
nums[2]=2;
for(i=3;i<=n;i++){
nums[i]=(nums[i-3]+nums[i-1]+nums[i-2])%1000000007;
}
return nums[n];
}
题目7 ID#62

一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?
例如,上图是一个7 x 3 的网格。有多少可能的路径?
示例 1:
输入: m = 3, n = 2
输出: 3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右
示例 2:
输入: m = 7, n = 3
输出: 28
提示:
1 <= m, n <= 100
题目数据保证答案小于等于 2 * 10 ^ 9
我的解答:
稍微复杂一点的动态规划题目,我们通过m = 3, n = 2的示例,可以看出
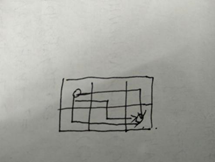
我们有三种方式到达终点,在坐标num[1][1]处,途经它的路径有两条,在num[i][0]和num[0][i]的边界中,都只有一条路径,而最后的终点的到达方式数=左边的格子的到达方式数+上面的格子的到达方式数
也就是等于2+1=3,图中也能清楚的看出来,实际上每一个位置(除左边界和上边界外,初始化为1)的到达方式数,都是当前位置左边的格子的到达方式数+上面的格子的到达方式数
动态规划方程为:dp[i][j]=dp[i-1][j]+dp[i][j-1],然后按原理写出代码
int uniquePaths(int m, int n){
int dp[n][m];
int i,j;
dp[0][0]=1;
for(i=0;i<m;i++){
dp[0][i]=1;
}
for(i=0;i<n;i++){
dp[i][0]=1;
}
for(i=1;i<n;i++){
for(j=1;j<m;j++){
dp[i][j]=dp[i-1][j]+dp[i][j-1];
}
}
return dp[n-1][m-1];
}
题目8 ID#64

给定一个包含非负整数的 m x n 网格,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例:
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。
我的解答:
从题目我们可以知道,对于一般的情况,我们想要到达该格子的数字总和最小,需要到达它的前一个格子的数字总和是最小的,而前一个格子有两种到达它的方式,上面和左面,取小的那个与当前格子的数字相加保存即可。特殊情况就是第一个格子,没有到达它的格子,它就是它本身,还有就是左边界线和上边界线,在这两个边界线上的格子能够到达他们的方式只有一种,要么就是没有更左边的格子,要么就是没有上边的格子,特殊情况列出即可
一般情况的动态规划方程是:grid[i][j]=grid[i][j]+min(grid[i-1][j],grid[i][j-1]);
int min(int a,int b){
return a<b?a:b;
}
int minPathSum(int** grid, int gridSize, int* gridColSize){
int i,j;
for(i=0;i<gridSize;i++){
for(j=0;j<gridColSize[i];j++){
if(i==0&&j==0){
continue;
}else if(i==0){
grid[i][j]=grid[i][j]+grid[i][j-1];
}else if(j==0){
grid[i][j]=grid[i][j]+grid[i-1][j];
}else{
grid[i][j]=grid[i][j]+min(grid[i-1][j],grid[i][j-1]);
}
}
}
return grid[gridSize-1][gridColSize[0]-1];
}
题目9 ID#120

给定一个三角形,找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。
例如,给定三角形:
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
说明:
如果你可以只使用 O(n) 的额外空间(n 为三角形的总行数)来解决这个问题,那么你的算法会很加分。
我的解答:
跟上一题的思路一样,一般情况的动态规划方程为:triangle[i][j]=min(triangle[i-1][j-1]+triangle[i][j],triangle[i-1][j]+triangle[i][j]);
然后判断一下特殊情况即可,因为最后我们是需要从上到下的最小路径和,所以我们在最底层寻找最小值,返回。
int min(int a,int b){
return a<b?a:b;
}
int minimumTotal(int** triangle, int triangleSize, int* triangleColSize){
int i,j;
for(i=0;i<triangleSize;i++){
for(j=0;j<triangleColSize[i];j++){
if(i==0&&j==0){
continue;
}else if(j==0){
triangle[i][0]=triangle[i][j]+triangle[i-1][0];
}else if(j==triangleColSize[i]-1){
triangle[i][j]=triangle[i][j]+triangle[i-1][triangleColSize[i-1]-1];
}else{
triangle[i][j]=min(triangle[i-1][j-1]+triangle[i][j],triangle[i-1][j]+triangle[i][j]);
}
}
}
int min=99999;
for(i=0;i<triangleColSize[triangleSize-1];i++){
if(triangle[triangleSize-1][i]<min){
min=triangle[triangleSize-1][i];
}
}
return min;
}
学习了评论区的解法,当我们从上到下进行计算路径和的时候,需要判断几种情况,但是由于这是三角形,我们可以从下至上来反向计算路径和,这样每一个位置的计算方式都是相同的:
triangle[i][j]=triangle[i][j]+min(triangle[i+1][j],triangle[i+1][j+1]);
最后返回triangle[0][0]即可
int min(int a,int b){
return a<b?a:b;
}
int minimumTotal(int** triangle, int triangleSize, int* triangleColSize){
int i,j;
for(i=triangleSize-2;i>=0;i--){
for(j=0;j<triangleColSize[i];j++){
triangle[i][j]=triangle[i][j]+min(triangle[i+1][j],triangle[i+1][j+1]);
}
}
return triangle[0][0];
}
题目10 ID122

给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: [7,1,5,3,6,4]输出: 7解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入: [1,2,3,4,5]输出: 4解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。
因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入: [7,6,4,3,1]输出: 0解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
我的解答:
因为卖出的那一天就可以再买入新的股票,然后我们考虑一下现实生活中想要在股市中一直赚钱的办法(假设我们能够预知股市),我们只需要在低点买入,高点卖出,在下跌的时候我们不持有股票,就可以一直赚钱。所以当前一天的股票价格比今天低的时候,证明股票是在上涨,我们买入前一天的股票,并且在今天卖出,当比今天高的时候,证明股票是在下跌,我们就不进行买入。
int maxProfit(int* prices, int pricesSize){
int tmp,sum=0,i;
for(i=1;i<pricesSize;i++){
tmp=prices[i]-prices[i-1];
if(tmp>0){
sum+=tmp;
}
}
return sum;
}
题目11 ID1346

给你一个整数数组 arr,请你检查是否存在两个整数 N 和 M,满足 N 是 M 的两倍(即,N = 2 * M)。
更正式地,检查是否存在两个下标 i 和 j 满足:
i != j
0 <= i, j < arr.length
arr[i] == 2 * arr[j]
示例 1:
输入:arr = [10,2,5,3]输出:true解释:N = 10 是 M = 5 的两倍,即 10 = 2 * 5 。
示例 2:
输入:arr = [7,1,14,11]输出:true解释:N = 14 是 M = 7 的两倍,即 14 = 2 * 7 。
示例 3:
输入:arr = [3,1,7,11]输出:false解释:在该情况下不存在 N 和 M 满足 N = 2 * M 。
提示:
2 <= arr.length <= 500
-10^3 <= arr[i] <= 10^3
我的解答:
首先想到的是暴力法直接遍历,寻找满足条件的解就返回true,否则返回false。
bool checkIfExist(int* arr, int arrSize){
int i,j;
if(arrSize==1||arrSize==0){
return false;
}
for(i=0;i<arrSize;i++){
for(j=i+1;j<arrSize;j++){
if(arr[i]==2*arr[j]||arr[j]==2*arr[i]){
return true;
}
}
}
return false;
}
题目12 ID234

请判断一个链表是否为回文链表。
示例 1:
输入: 1->2输出: false
示例 2:
输入: 1->2->2->1输出: true
进阶:
你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题?
我的解答:
感觉做过的,但是leetcode上面显示没做过,就当复习吧。
采用快慢指针寻找链表中点,然后从中点处将后半段链表进行反转,反转之后的两个链表依次进行比较,如果有一位不相同,则返回false,否则返回true
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
bool isPalindrome(struct ListNode* head){
struct ListNode* fast=head,*sen=head;
while(fast&&fast->next){
fast=fast->next->next;
sen=sen->next;
}
fast=head;
struct ListNode *p=sen,*q=NULL;
while(sen){
p=sen;
sen=p->next;
p->next=q;
q=p;
}
sen=p;
while(sen&&fast){
if(sen->val!=fast->val){
return false;
}
sen=sen->next;
fast=fast->next;
}
return true;
}
题目13 ID1013

给你一个整数数组 A,只有可以将其划分为三个和相等的非空部分时才返回 true,否则返回 false。
形式上,如果可以找出索引 i+1 < j 且满足 (A[0] + A[1] + ... + A[i] == A[i+1] + A[i+2] + ... + A[j-1] == A[j] + A[j-1] + ... + A[A.length - 1]) 就可以将数组三等分。
示例 1:
输出:[0,2,1,-6,6,-7,9,1,2,0,1]输出:true解释:0 + 2 + 1 = -6 + 6 - 7 + 9 + 1 = 2 + 0 + 1
示例 2:
输入:[0,2,1,-6,6,7,9,-1,2,0,1]输出:false
示例 3:
输入:[3,3,6,5,-2,2,5,1,-9,4]输出:true解释:3 + 3 = 6 = 5 - 2 + 2 + 5 + 1 - 9 + 4
提示:
3 <= A.length <= 50000
-10^4 <= A[i] <= 10^4
我的解答:
修修补补还是通过了,想要将整数数组A划分为三个和相等的非空部分,首先这个整数数组的和就需要能够整除3,然后我们使用双指针法,i,j分别指向数组的头部和尾部,分别计算其遇到元素的和,当头尾指针遍历数组时的和与整数数组总的和/3相等,同时i<=j(因为i,j指针指向元素分别跟首尾的和相加之后,令i++,j--,所以i,j最后指向的元素并非最后相加的元素,故这里取等号)时,证明是可以划分成三个和相等的非空部分的,第三个非空部分就是两个指针的中间部分,sum_3是整数数组总和/3之后的结果,条件判断中有sum_3==0,是为了防止出现[1,-1,-1,1]这种案例时,首尾和sum_1,sum_2直接与sum_3相等即等于0。
bool canThreePartsEqualSum(int* A, int ASize){
int i,j;
int sum=0;
int sum_1=0,sum_2=0,sum_3=0;
for(i=0;i<ASize;i++){
sum+=A[i];
}
if(sum%3!=0){
return false;
}else{
sum_3=sum/3;
}
for(i=0,j=ASize-1;i<=j;){
if(sum_1!=sum_3||sum_3==0){
sum_1+=A[i];
i++;
}
if(sum_2!=sum_3||sum_3==0){
sum_2+=A[j];
j--;
}
//printf("%d %d %d %d
",sum_1,sum_2,i,j);
if(i<=j&&sum_1==sum_3&&sum_2==sum_3){
//printf("%d %d",i,j);
return true;
}
}
return false;
}
题目14 ID面试题 16.11

你正在使用一堆木板建造跳水板。有两种类型的木板,其中长度较短的木板长度为shorter,长度较长的木板长度为longer。你必须正好使用k块木板。编写一个方法,生成跳水板所有可能的长度。
返回的长度需要从小到大排列。
示例:
输入:
shorter = 1
longer = 2
k = 3输出: {3,4,5,6}
提示:
0 < shorter <= longer
0 <= k <= 100000
我的解答:
列举出短木板和长木板在k的数量限制下的全部组合长度,因为是从小到大排序,所以我们也从短木板开始计算长度,另外需要考虑k=0和shorter=longer两种特殊情况,python2编写
class Solution(object):
def divingBoard(self, shorter, longer, k):
"""
:type shorter: int
:type longer: int
:type k: int
:rtype: List[int]
"""
rlist=[]
if k==0:
return rlist
if shorter==longer:
rlist.append(shorter*k)
return rlist
else:
for i in range(0,k+1):
sum1=shorter*(k-i)+longer*(i)
rlist.append(sum1)
return rlist
题目15 ID172

给定一个整数 n,返回 n! 结果尾数中零的数量。
示例 1:
输入: 3输出: 0解释: 3! = 6, 尾数中没有零。
示例 2:
输入: 5输出: 1解释: 5! = 120, 尾数中有 1 个零.
说明: 你算法的时间复杂度应为 O(log n) 。
我的解答:
最开始的代码是这样的,但是long long的数据类型都溢出了,而且没有使用递归的方法
int trailingZeroes(int n){
int flag=0,i;
long long sum=1;
for(i=2;i<=n;i++){
sum*=i;
}
while(sum%10==0){
flag++;
sum/=10;
}
return flag;
}
所以这道题肯定不是想让我们用这种方法做出来,思考为什么n!结果中会出现零,举几个例子,3!是3*2*1=6,没有0,5!=5*4*3*2*1=120,末尾有一个0,而零的出现是因为5*2,或者是5*4而导致的,4可以分解成2*2。而10!=1*2*3*4*5*6*7*8*9*10,考虑偶数的话,可以分解为:2*4*6*8*10,再分解:2*(2*2)*(2*3)*(2*2*2)*(2*5),分解之后有一个5,原来的奇数中还有一个5,他们跟2匹配,所以10!=3628800,末尾有两个0,可以发现阶乘中有几个2,5的配对,就有几个0,但是2很容易能够分解出来,也就是说2的数量总是大于5的数量,像前几个例子里面,所以我们只需要考虑给我们的n中有几个5的倍数,就能够知道阶乘后有几个0了。
有思路之后编写代码为:
int trailingZeroes(int n){
int count=0;
while(n>=5){
count+=n/5;
n/=5;
}
return count;
}
