[最优化理论与技术]预备知识

预备知识

目录

• 预备知识
  • 课程内容
  • 预备知识
  • 最优化问题
    • 数学表示
    • 分类
  • 多元函数的Taylor公式
    • 多元函数的梯度
    • 多元函数的极值与Hessian矩阵
    • 泰勒展开式
  • 凸集、凸函数和凸优化问题
    • 凸集
    • 凸函数
    • 凸优化
  • 补充内容
    • 仿射集 (affine set)
    • 锥 (cone)
    • 正定矩阵
    • 隐函数求导
    • 方向导数与梯度
    • 一维搜索的方法
    • 裴波那契法(Fibonacci法)
    • 黄金分割法
    • 牛顿法

课程内容

1. 预备知识
2. 线性规划
3. 一维搜索方法
4. 无约束最优化方法
5. 约束最优化方法
6. 工程应用优化

预备知识

1. 最优化问题
2. 多元函数的Taylor公式
3. 多元函数极值问题
4. 凸集、凸函数和凸优化
5. 算法相关概念
6. 算法概述

最优化问题

数学表示

[minf(x)\s.t quad c(x)ge 0 ]

• (x=(x_1,x_2,...,x_n))是一个包含多变量的向量：决策变量
• (c(x))是对各个变量约束的等式和不等式：约束条件
  • 可行域：约束条件在空间围成的区域
  • 可行解：可行域中每个点都是原问题的可行点
• (f(x))：目标函数
  • 最优解：能使目标函数达到最大或最小的可行解

分类

按约束

• 无约束
• 有约束
  • 等式约束
  • 不等式约束

按目标函数

• 线性规划
• 非线性规划

按函数变量

• 整数规划
• 非整数规划

按目标函数个数

• 单目标优化
• 多目标优化

多元函数的Taylor公式

多元函数的梯度

偏导：多元函数降维时的变化，比如二元函数固定(y)，只让(x)单独变化，从而看成关于(x)的一元函数的变化

[f_x(x,y)=lim_{Delta x o 0}frac{f(x+Delta x,y)-f(x,y)}{Delta x} ]

记作(frac{partial f(x,y)}{partial x})

梯度：多元函数在(A)点无数个变化方向中变化最快的那个方向；每一个变量都沿着关于这个变量的偏导所指定的方向来变化，函数的整体变化就能达到最大 (变化的绝对值最大) 。

[gradA=(f_x(A),f_y(A),f_z(A)) ]

多元函数的极值与Hessian矩阵

参考Hessian矩阵与多元函数极值

一元函数极值问题：(f(x)=x^2)，先求一阶导数(f'(x)=2x)，根据费马定理极值点处的一阶导数一定等于0。

• 费马定理给出的是必要条件，由一阶导数=0可推出该店为极值，但不能由极值推出一阶导数=0
• 对该二次函数，一阶导数=0求得极值，但对(f(x)=x^3)，只检查一阶导数是不足以推出结果的
• 对(f(x)=x^3)，再求二阶导数，如果(f''<0)，说明函数在该点取得局部极大值；如果(f''>0)，说明函数在该点取得局部极小值；如果(f''=0)，说明结果任然不确定，需要其他方式确定函数极值

多元函数极值问题：(f=f(x,y,z))，首先对每一个变量分别求偏导数，求得函数的可能极值点

[frac{partial f}{partial x}=0\frac{partial f}{partial y}=0\frac{partial f}{partial z}=0 ]

接下来，继续求二阶导数，包含混合偏导共9个偏导函数，用矩阵表示得到

[H=left[egin{matrix}frac{partial ^2f}{partial x partial x} & frac{partial ^2 f}{partial x partial y } & frac{partial ^2 f}{partial x partial z } \ frac{partial ^2f}{partial y partial x} & frac{partial ^2 f}{partial y partial y } & frac{partial ^2 f}{partial y partial z } \ frac{partial ^2f}{partial z partial x} & frac{partial ^2 f}{partial z partial y } & frac{partial ^2 f}{partial z partial z}end{matrix} ight] ]

矩阵(H)就是一个三阶Hessian矩阵。扩展到一般情况，对一个在定义域内二阶连续可导的实质多元函数(f(x_1,x_2,...,x_n))定义其Hessian矩阵(H)如下

[H=left[egin{matrix}frac{partial ^2f}{partial x_1 partial x_1} & frac{partial ^2 f}{partial x_1 partial x_2 } & dots &frac{partial ^2 f}{partial x_1 partial x_n } \ frac{partial ^2f}{partial x_2 partial x_1} & frac{partial ^2 f}{partial x_2 partial x_2 } & dots & frac{partial ^2 f}{partial x_2 partial x_n } \ vdots & vdots & ddots & vdots \frac{partial ^2f}{partial x_n partial x_1} & frac{partial ^2 f}{partial x_n partial x_2 } & dots & frac{partial ^2 f}{partial x_n partial x_n}end{matrix} ight] ]

当一元函数的二阶导数=0，不能确定函数在该点的极值性。类似地，当Hessian矩阵行列式=0，也不能断定多元函数极值性的情况。甚至可能得到一个鞍点，也就是一个既非极大值也非极小值的点。

基于Hessian矩阵，可判断多元函数极值情况如下：

1. 如果Hessian矩阵是正定矩阵，则临界点处是一个局部极小值
2. 如果Hessian矩阵是负定矩阵，则临界点处是一个局部极大值
3. 如果Hessian矩阵是不定矩阵，则临界点处不是极值

判断矩阵是否正定：

1. 顺序主子式；实对称矩阵为正定矩阵的充要条件是的各顺序主子式都大于零
2. 特征值；实二次型矩阵为正定二次型的充要条件是的矩阵的特征值全大于零；负定二次型的充要条件是的矩阵的特征值全小于零；否则是不定的

泰勒展开式

一元函数的泰勒公式：设一元函数(f(x))在包含点(x_0)的开区间((a,b))内具有(n+1)阶导数，则当(x in (a,b))时，(f(x))的(n)阶泰勒公式为：

[f(x)=f(x_0)+f'(x_0)(x-x_0)+frac{f''(x_0)}{2!}(x-x_0)^2+...+frac{f^{(n)}(x_0)}{n!}(x-x_0)^n+R_n(x) ]

其中，(R_n(x))的拉格朗日余项表达形式

[R_n(x)=frac{f^{(n+1)}(xi)}{(n+1)!}(x-x_0)^{n+1}quad xi in (x,x_0) ]

(R_n(x))的皮亚诺余项表达形式

[R_n(x)=o[(x-x_0)^n] ]

二元函数的泰勒公式：设二元函数(z=f(x,y))在点((x_0,y_0))的某一领域内连续且有直到(n+1)阶的连续偏导数，则有

[f(x,y)=f(x_0,y_0)+[(x-x_0)frac{partial}{partial x}+(y-y_0)frac{partial}{partial y}]f(x_0,y_0)+\ frac{1}{2!}[(x-x_0)frac{partial}{partial x}+(y-y_0)frac{partial}{partial y}]^2f(x_0,y_0)+...\ +frac{1}{n!}[(x-x_0)frac{partial}{partial x}+(y-y_0)frac{partial}{partial y}]^nf(x_0,y_0)\+R_n(x,y) ]

其中，记号

[(x-x_0)frac{partial}{partial x}+(y-y_0)frac{partial}{partial y}]f(x_0,y_0) ]

表示

[(x-x_0)f_x(x_0,y_0)+(y-y_0)f_y(x_0,y_0) ]

记号

[[(x-x_0)frac{partial}{partial x}+(y-y_0)frac{partial}{partial y}]^2f(x_0,y_0) ]

表示

[(x-x_0)^2f_{xx}(x_0,y_0)+2(x-x_0)(y-y_0)f_{xy}(x_0,y_0)+(y-y_0)^2f_{yy}(x_0,y_0) ]

一般地，记号

[[(x-x_0)frac{partial}{partial x}+(y-y_0)frac{partial}{partial y}]^mf(x_0,y_0) ]

表示

[sum_{p=0}^m C_m^p(x-x_0)^p(y-y_0)^{(m-p)} frac{partial^m f}{partial x^ppartial y^{(m-p)}}|_{(x_0,y_0)} ]

用一般化表达式重写上面的式子

[f(x,y)=sum_{k=0}^nfrac{1}{k!}[(x-x_0)frac{partial}{partial x}+(y-y_0)frac{partial}{partial y}]^kf(x_0,y_0)\ +R_n(x,y) ]

拉格朗日余项为：

[R_n(x,y)=frac{1}{(n+1)!}[(x-x_0)frac{partial}{partial x}+(y-y_0)frac{partial}{partial y}]^{(n+1)}f(x_0+ heta(x-x_0),y_0+ heta(y-y_0))\ heta in (0,1) ]

皮亚诺余项为：

[R_n(x,y)=o( ho^n) ]

Hessian矩阵与泰勒展开的关系：对于一个多维向量(X)，多元函数(f(X))在点(X_0)的领域内有连续二阶偏导数，可写出(f(X))在点(X_0)处的二阶泰勒展开式

[f(mathbf{X})=f(mathbf{X}_0)+(mathbf{X}-mathbf{X}_0)^T abla f(mathbf{X}_0)+frac{1}{2!}(mathbf{X}-mathbf{X}_0)^T abla^2 f(mathbf{X}_0)(mathbf{X}-mathbf{X}_0)+o(|mathbf{X}-mathbf{X}_0|^2) ]

而( abla^2 f(mathbf{X}_0))显然是一个Hessian矩阵，所以可写成：

[f(mathbf{X})=f(mathbf{X}_0)+(mathbf{X}-mathbf{X}_0)^T abla f(mathbf{X}_0)+frac{1}{2}(mathbf{X}-mathbf{X}_0)^Tmathbf{H}(mathbf{X}_0)(mathbf{X}-mathbf{X}_0)+o(|mathbf{X}-mathbf{X}_0|^2) ]

1. 多元函数取得极值的必要条件：(u=f(x_1,x_2,...,x_n))在点(M)处有极值，则有

   [ abla f(M)=left {frac{partial f}{partial x_1},frac{partial f}{partial x_2},cdots, frac{partial f}{partial x_n} ight}_M=0 ]

2. 多元函数取得极值的充分条件：其二阶偏导组成的Hessian矩阵为正定(局部极小值)or负定(局部极大值)

凸集、凸函数和凸优化问题

凸集

集合(C)内任意两点间的线段也在集合(C)内，则称集合(C)为凸集:

[lambda x +(1-lambda)y in Cquad for quad forall lambda in (0,1),quad forall(x,y)in C ]

凸函数

定义在凸集(C)上的凸函数：

[f(lambda x_1+(1-lambda)x_2)le lambda f(x_1)+(1-lambda)f(x_2) \x_1,x_2 in C;quad lambda in (0,1) ]

凸优化

机器学习主要做的就是优化问题，先初始化一下权重参数，然后利用优化方法来优化权重，直到准确率不再上升，迭代停止。在优化问题中，应用最广泛的是凸优化问题：

• 若可行域是凸集
• 且目标函数是一个凸函数

则这样的优化问题是凸优化问题

补充内容

仿射集 (affine set)

欧式空间 (R^n) 中的点集 (M)，对于(forall x,y in M)，以及 (forall lambda)，总有：

[(1-lambda)x+lambda y in M ]

则点集 (M) 是仿射集。

几何意义：仿射集的几何意义是：一个集合中任意两点的连线上的点仍然属于这个集合。（在三维空间内，整个坐标系才属于仿射集）

例：

• 三维欧氏空间 (R^3) 中，直线和平面都是仿射集，空集 (varnothing) 也是仿射集
• (S) 是 (R^n) 中的子空间的充要条件是 (S) 是包含原点的仿射集
• 每一非空仿射集 (S) 都平行于唯一子空间 (L)
  • 集合平移：(S+p={ x+p|x in S })
• 非空仿射集 (S) 的维数是与它平行的子空间的维数，(dim(S))
• 维数为 0，1，2 的仿射集就是熟知的点、线、面
• (R^n) 中的 (n-1) 维仿射集称为超平面 (hyperplane)

锥 (cone)

参考：锥，凸锥，二阶锥，二阶锥规划

对于一个向量空间 (V) 与它的一个子集 (C)，如果子集 (C) 中任意一点 (x) 与任意正数 (a)

，其乘积 (ax) 仍然属于子集 (C)，则称 (C) 为一个锥。

锥总是无界的。

凸锥：锥 (C) 中任意两点 (x) 和 (y)，(ax+by in Cquad(a,b>0))

• 凸锥首先是凸集
• 不是凸锥的锥，eg：(y=|x|)，但是 (y ge |x|) 就是凸锥

正定矩阵

• 对于 (n*n) 实对称矩阵： (M)满足任意非零实系数向量 (x)，都有 (x^TMx>0)，则 (M) 是正定的
• 对于复数矩阵：一个 (n*n) 的 (Hermite) 矩阵 (M) 是正定的当且仅当任意非零复向量 (x)，都有 (x^HMx>0)。
  • 前提要是 (Hermite) 矩阵，满足 (M^H=M)

隐函数求导

隐函数：如果方程 $F(x,y=0) $ 能确定 (y) 是 (x) 的函数，那么称这种函数表达方式为隐函数。(已知函数关系，不容易写出显函数形式)

1. 表示成关于 (y) 的函数，链式求导
2. 将待求导变量放到等式一边，等式两边同时求导
3. 隐函数保存不变，直接对等式两边求导

方向导数与梯度

参考：[梯度下降（Gradient Descent）小结]

一维搜索的方法

Line Search (一维搜索，或线搜索、一维优化) 是最优化 (Optimization) 算法中的一个基础步骤，是求解一维目标函数 (f(x)) 最优解的过程。可以分为精确的一维搜素和不精确的一维搜素两大类。

当采用数学规划法寻求多元函数极值点时，一般需进行如下格式的迭代计算：$$x^{k+1}=x{k}+alpha_ks^k(k=0,1,2,...)$$

当方向 (s^k) 给定，求最佳步长 (alpha_k) 就是求一元函数：

[f(x^{k+1})=f(x^k+alpha_ks^k)=phi(alpha_k) ]

的极值问题，这一过程被称为一维搜索

裴波那契法(Fibonacci法)

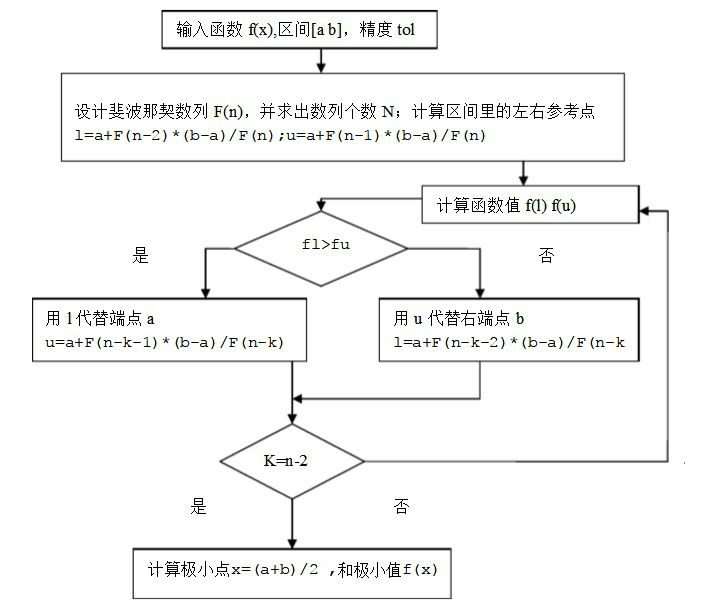
在区间 ([a,b]) 内取两个不同点，算出函数值加以比较，逐步缩小搜索区间。

单峰函数

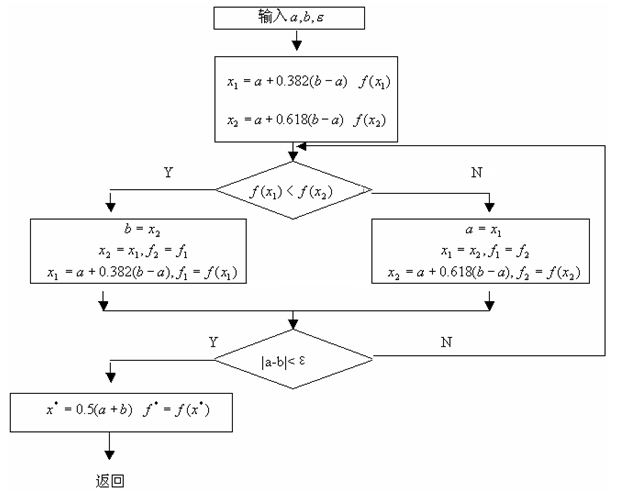
黄金分割法

牛顿法

切线是曲线的线性逼近

多次迭代后会越来越接近曲线的根

对于非线性函数 (f(x))，根据泰勒公式得到 (x) 附近某个点(x_{k})展开的多项式可用来近似函数 (f(x)) 的值，该多项式对应的函数为 (F(x))，求得 (F(x)) 的极小值作为新的迭代点，然后继续在新的迭代点泰勒公式展开，直到求得的极小值满足一定的精度。

原理：

假设函数 (f(x)) 二次可微，则二阶泰勒展开：

[f(x)approx g(x)=f(x_k)+f'(x_k)(x-x_k)+frac{1}{2}f''(x_k)(x-x_k)^2 ]

(g(x)) 与 (f(x)) 近似，求函数 (f(x)) 的极值转化为求导函数为0，对 (g(x)) 求导并令等于0，

[f'(x_k)+f''x_k(x-x_k)=0 ]

得：

[x=x_k-frac{f'(x_k)}{f''(x_k)} ]

得迭代公式：

[x_{k+1}=x_k-frac{f'(x_k)}{f''(x_k)} ]

代码：

参考：机器学习之牛顿法

def h(x):
    return x*x*x + 2*x*x +3*x + 4

def h1(x):
    return 3*x*x + 4*x + 3

def h2(x):
    return 6*x + 4

xk = 0
k = 1
y = 0
e = 0.0001
times = 10000

while k < times:
    y = h(xk)
    a = h1(xk)
    if abs(a) <= e:
        break
    b = h2(xk)
    xk -= a/b
    k += +1
print("k = ", k)
print("x = ", xk)
print("y = ", y)