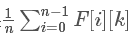[概率dp] Jzoj P4212 我想大声告诉你

Description

因为小Y 是知名的白富美，所以自然也有很多的追求者，这一天这些追求者打算进行一次游戏来踢出一些人，小R 自然也参加了。
这个游戏有n 个人参加，每一轮随机选出一个还没有出局的人x，接着x 会出局。x 在出局之后剩下的人会受到一次攻击，每一个人在遭到攻击之后会有p 的概率出局。（注意遭到攻击出局的人是不能攻击剩下的人的）
在所有人都出局之后，遭受攻击次数等于特定值的人能够成为胜者。所以现在小R 想要知道对于每一个0 <= k < n，自己恰好在遭受k 次攻击之后出局的概率是多少。（这里的出局指的不是被攻击出局）
注意在这题中，所有数值的运算在模258280327 的意义下进行。

 

Input

第一行输入一个正整数T 表示数据组数。
对于每一组数据输入仅一行三个数n, x, y，表示在这组数据中有n 个人参赛，p = x/y。保证y 和258280327 互质。

Output

对于每组数据，输出一行n 个整数，表示对于k = 0到n - 1 的概率在模258280327 意义下的值。

 

Sample Input

2
3 40 100
9 32 1049

Sample Output

172186885 92980918 16529941
229582513 163885050 39458156 102374877 116777758 216371874 55544199 95860736 8136787

 

Data Constraint

对于60% 的数据，n <=100
对于100% 的数据，n <= 2* 10^3，1 <= T <= 5，0<= x < y <= 10^9

题解

• 题目大意：n个人包括主人公小R，每轮会随机等概率的踢走一个人，而剩下的人每人会有x/y的概率被干掉，而被干掉的人不能攻击剩下的人，问小R在每轮出局的概率为多少
• 首先，我们可以知道这个问题至于小R小童鞋有关系，而剩下的n-1的小童鞋可以是等价的，也就是可以不用管它们
• 先想想部分分的做法，对于60%的数据，我们可以设f[i][j]为剩下i个人，被攻击了j轮的概率
• 那么就可以分成两种情况，一种是被钦定出局，一种是被干掉
• 对于第一种直接*1/i就好了，那么对于第二种情况，可以枚举一下这次攻击会有多少个人干出局，然后算概率就好了
• 再回来考虑一下100分做法：
• 因为我们知道其实其他的n-1的小童鞋是等价的，不如我们就钦定它是按顺序踢人走的
• 同样的设f[i][j]为剩下i个人，被攻击了j轮的概率
• 那么我们还是两种情况，一种就是正常出局，那么我们是很坚强的忍受了j-1轮的严刑拷打，f[i][j]=f[i-1][j-1]*(1-p)^(j-1)
• 另一种就是被打出去，那么我们就不能对剩下的人有任何的贡献，f[i][j]=f[i-1][j]*(1-(1-p)^j))
• 考虑一下答案究竟是啥子东东，那么可以知道对于每一轮剩下多少个人都是有可能的
• 这样的话，若j是固定，那就是

代码

#include <cstdio>
#include <cstring>
#define ll long long
using namespace std;
const ll N=200,mo=258280327;
int n,Q;
ll x,y,k,sum,ny[N],f[N][N],r,p;
ll ksm(ll a,ll b){ for (r=1;b;b>>=1,a=a*a%mo) if (b&1) r=r*a%mo; return r; }
int main()
{
    scanf("%d",&Q);
    while (Q--)
    {
        scanf("%d%lld%lld",&n,&x,&y),memset(f,0,sizeof(f)),f[1][0]=1,k=ksm(y,mo-2),p=ksm(n,mo-2),ny[0]=1;
        for (int i=1;i<=n;i++) ny[i]=ny[i-1]*(y-x)%mo*k%mo;
        for (int i=1;i<=n-1;i++)
            for (int j=0;j<=n-1;j++)
                if (f[i][j]) f[i+1][j+1]=(f[i+1][j+1]+f[i][j]*ny[j+1]%mo)%mo,f[i+1][j]=(f[i+1][j]+f[i][j]*(1-ny[j]+mo)%mo)%mo;
        for (int j=0;j<=n-1;j++,sum=0)
        {
            for (int i=1;i<=n;i++) (sum+=f[i][j])%=mo;
            printf("%lld ",sum*p%mo);
        }
        printf("
");
    }
}