题解
- 题目大意:问有n个班,每个班有a[i]个人,问相邻两个人都不同班的方案数
- n<=50,∑Ai<=1500,极其优秀的范围,考虑一下dp,设f[i][j]表示做到前i个班,有j个相邻为同班为位置的方案数
- 首先,根据样例我们可以得出,每个班的每个人互换位置也算一种方案数,那么我们先考虑每个班里的人都是火柴人
- 那么这个dp的状态转移方程为
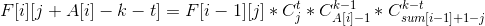
- 就是将A[i]分成k组,将t组插入分配到之前j个相邻的位置中,
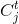 就是将t组分配插入到j个位置的方案数,
就是将t组分配插入到j个位置的方案数,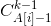 就是将A[i]分成k组的方案数(就是挡板问题),
就是将A[i]分成k组的方案数(就是挡板问题),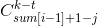 就是将剩下的k-t组分配到剩下的原来合法的位置中的方案数
就是将剩下的k-t组分配到剩下的原来合法的位置中的方案数
- 然后怎么求呢,显然就可以预处理出组合数(杨辉三角)和阶乘(等下就知道了),答案就是F[n][0]
- 那么我们返回来求每个班内不同人的分配,就是排列问题嘛,就是a[i]!
- 所以最后的答案就为

代码
1 #include <cstdio>
2 #include <iostream>
3 #include <cstring>
4 #define ll long long
5 #define N 60
6 #define M 1510
7 #define mo 1000000007
8 using namespace std;
9 int n;
10 ll a[N],sum[N],f[N][M],jc[M],c[M][M],ans;
11 int main()
12 {
13 freopen("photo.in","r",stdin),freopen("photo.out","w",stdout),scanf("%d",&n);
14 for (int i=1;i<=n;i++) scanf("%lld",&a[i]),sum[i]=sum[i-1]+a[i];
15 jc[0]=c[0][0]=1; for (int i=1;i<=1500;i++) jc[i]=jc[i-1]*i%mo;
16 for (int i=1;i<=1500;i++)
17 {
18 c[i][0]=c[i][i]=1;
19 for (int j=1;j<=i-1;j++) c[i][j]=(c[i-1][j]+c[i-1][j-1])%mo;
20 }
21 f[1][sum[1]-1]=1;
22 for (int i=2;i<=n;i++)
23 for (int j=0;j<=sum[i-1];j++)
24 if (f[i-1][j])
25 for (int k=1;k<=a[i];k++)
26 for (int p=0;p<=min(k,j);p++)
27 (f[i][j-p+a[i]-k]+=f[i-1][j]*c[j][p]%mo*c[a[i]-1][k-1]%mo*c[sum[i-1]+1-j][k-p]%mo)%=mo;
28 ans=f[n][0];
29 for (int i=1;i<=n;i++) ans=ans*jc[a[i]]%mo;
30 printf("%lld",ans);
31 }
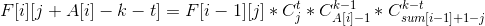
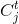 就是将t组分配插入到j个位置的方案数,
就是将t组分配插入到j个位置的方案数,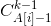 就是将A[i]分成k组的方案数(就是挡板问题),
就是将A[i]分成k组的方案数(就是挡板问题),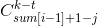 就是将剩下的k-t组分配到剩下的原来合法的位置中的方案数
就是将剩下的k-t组分配到剩下的原来合法的位置中的方案数