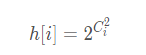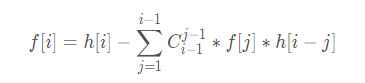[dp][数学] Jzoj P5923 Bomb

Description

         常数国与 Hack 国近年来战火纷飞。
         常数国共有 n 个城市，每两个城市之间均有一条交通线联通。如今常数国遭到 Hack 国的重创，岌岌可危。Hack 国国王小 K 决定轰炸常数国的交通线，对常数国发起最后的攻击。
         面对危难之时，常数国国王决定更换首都。在 Hack 国的轰炸结束之后，常数国的领土将会分成若干个联通块。常数国的首都，将会从联通块大小最大的联通块中，随机选择一个城市，作为首都。
         小 K 得知了常数国的应对方案之后，他想知道，Hack 国有多少种不同的轰炸方案，使得常数首都所在的联通块大小恰好为 k。两种轰炸方案是不同的，当且仅当一条交通线在一种方案中存在，在另一种方案中被轰炸。由于方案数可能很大，你需要输出方案数对 998,244,353 取模的结果。

 

Input

从文件bomb.in中读入数据。
共一行，两个整数 n,k ，表示常数国城市的个数与首都所在联通块大小。

Output

输出到文件bomb.out中。
共一行，表示 Hack 国的轰炸方案数对 998,244,353 取模后的结果。

 

Sample Input

​Sample Input 1
3 2



Sample Input 2
5 3


Sample 3
见选手目录下的bomb/bomb3.in与bomb/bomb3.ans。
该组样例的数据范围同第 8 个测试点。

Sample Output

Sample Output1
3

Explanation
3 种方案分别为，仅保留 1 号城市与 2 号城市的交通线，仅保留 2 号城市与3 号城市的交通线，仅保留 1 号城市与 3 号城市的交通线。

Sample Output2
80

 

 

Data Constraint

对于 100% 的数据，满足 1 ≤ k ≤ n ≤ 2 × 10 3 。除此之外，对于每个数据点，还满足以下限制。

 

题解

• 考虑一下dp
• 设f[i]为大小为i的联通块的个数，h[i]为大小为i的图的个数
• 其实转移状态很显然
• 
• 
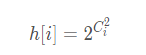
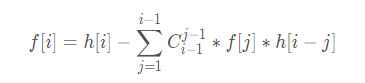
• 可以设dp[i][j]为大小为i的图的个数，j=1有联通块等于k，j=0所有联通块小于k
• 状态转移方程为
• 

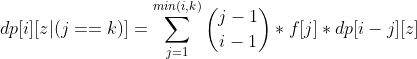
代码

#include <cstdio>
#include <iostream>
#define N 2010
#define mo 998244353
using namespace std;
int n,k;
long long mi[N*N],f[N][2],F[N],g[N],c[N][N];
int main()
{
    scanf("%d%d",&n,&k);
    mi[0]=1; for (int i=1;i<=n*n;i++) mi[i]=mi[i-1]*2%mo;
    c[0][0]=1;
    for (int i=1;i<=n;i++)
    {
        c[i][0]=1;
        for (int j=1;j<=i;j++) c[i][j]=(c[i-1][j]+c[i-1][j-1])%mo;
    }
    F[1]=0,g[1]=1;
    for (int i=2;i<=n;i++)
    {
        for (int j=1;j<=i-1;j++) F[i]=(F[i]+g[j]*(g[i-j]+F[i-j])%mo*c[i-1][j-1]%mo)%mo;
        g[i]=(mi[i*(i-1)/2]-F[i]+mo)%mo;
    }
    memset(f,0,sizeof(f)),f[0][0]=1;
    for (int i=1;i<=n;i++)
        for (int j=1;j<=k;j++)
            if (i-j>=0)
                for (int z=0;z<=1;z++)
                    f[i][z|(j==k)]=(f[i][z|(j==k)]+f[i-j][z]*g[j]%mo*c[i-1][j-1]%mo)%mo;
    printf("%lld",f[n][1]);
}