
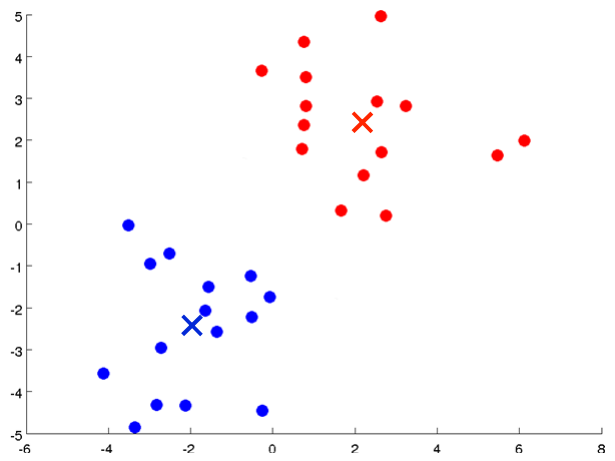

K-means算法是一种迭代算法,步骤如下:
1.随机初始化K个聚类中心u1,u2,...,uk
2.根据每个样本和各个聚类中心的距离给每个样本打上标签(例如,x(i)与u3的距离最小,则x(i)的标签为3)
3.计算每个类别的样本的中心(通过均值来计算),更新每个聚类中心的位置
4.重复步骤2、3直到收敛

以上的J函数也成为失真函数,是每个样本点到对应中心距离的平方的均值。

随机初始化时从样本中选出K个样本作为初始的聚类中心是一个常用的初始化方式。
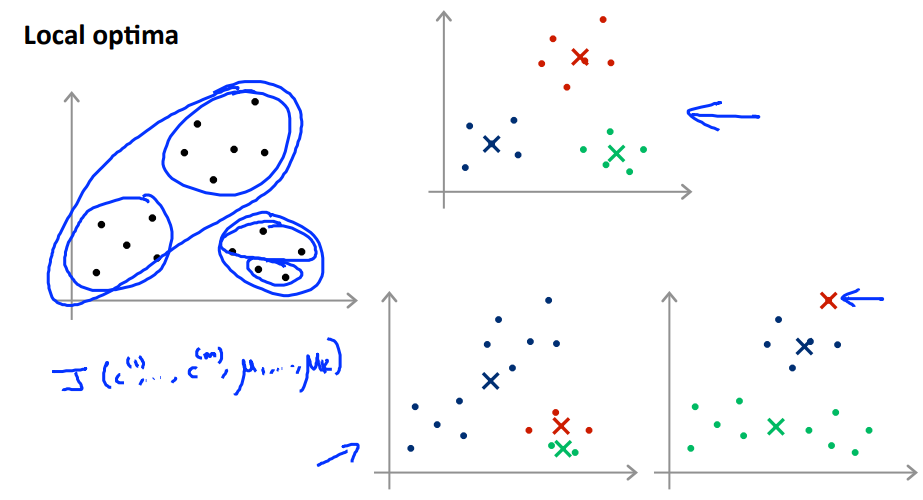

通过多次(50,100...)随机初始化来避免得到的是局部最优解。
多次初始化后得到不同的失真函数值J,选J值最小的一个,这样会更接近全局最优解。
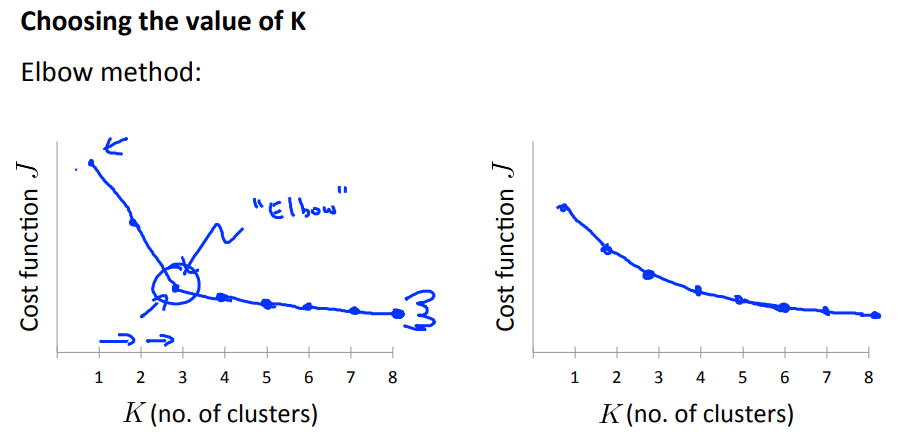
当不知道样本应该分成多少类时,如何选择合适的分类数量K?
1.通过肘部方法(Elbow method),如上图左侧,当失真函数有一个明显的转折的时候,这个转折点的分类数量是合适的分类数量。
不过大多数情况下失真函数回事上图右侧的情况,是一个平滑下降的过程,没有明显的转折点,这时候肘部方法就不适用。

例如上图中的T恤尺寸问题,分成三类还是五类好呢?当上面的肘部方法也不适用的时候,可以参考一下后续销售专家的意见。
是分成3类以更便宜的价格卖好呢?还是提供更多的尺寸卖好呢?