洛谷 2409 dp 月赛题目

#洛谷 2409 dp

洛谷十月月赛T1，一道有些interesting的dp题目，当时做的时候想的比较复杂，根本没有往dp的方向去想。。

非官方题解：

1、据说可以使用优先队列来处理，参见Uva11997
2、据说可以二分sum值再搜索剪枝，然而个人实现只得了50分

正解：

设dp[i][j]表示使用了前i个盒子，组成的sum值为j的方案数

首先预处理出dp[1][] 的值，之后进行转移，对于第i个盒子，dp[i][j] = (dp[i][j] + dp[i-1][j + data[i][k]])

借用一下kkk的图

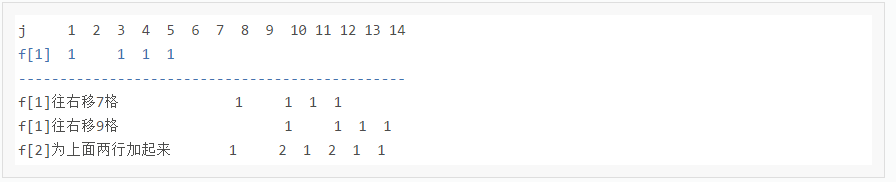
通俗点解释，假设第一个盒子为1 3 4 5，则dp[1][1] = dp[1][3] = dp[1][4] = dp[1][5] = 1，

考虑第二个盒子为1 7 9， 则dp[2][1 + 1] += 1, dp[2][3 + 1] += 1, dp[2][4 + 1] += 1, dp[2][5 + 1] += 1,
dp[2][1 + 7] += 1, dp[2][3 + 7] += 1 ... 以此类推

由此得证dp方程

小优化：

（时间）显然可以发现每次sum值最多只会增加100，可以以此限定j的上限。
（空间）由于第一维满足滚动数组的使用条件，可使用滚动数组压缩掉一维的空间

#include <cstdio>
#include <algorithm>
#include <cstring>


int dp[110][10100];
int x;
int n;
int mi;
int k;
int tot = 0;
int main () {
    scanf("%d %d", &n, &k);
    scanf("%d", &mi);
    tot += 100;
    for (int i = 1; i <= mi; i++) {
        scanf("%d", &x);
        dp[1][x]++ ;
    }
    for (int i = 2; i <= n; i++) {
        tot += 100;
        scanf("%d", &mi);
        for (int j = 1; j <= mi; j++) {
            scanf("%d", &x);
            for (int k = 0; k <= tot; k++) dp[i][k + x] += dp[i-1][k];
        }
    }
    for (int i = 1; i <= tot; i++) {
        while (dp[n][i] > 0) {
            k--;
            dp[n][i]--;
            printf("%d ", i);
            if (k == 0) return 0;
        } 
    }


    return 0;
}