由于分类问题的输出是0、1这样的离散值,因而回归问题中用到的线性回归模型就不再适用了。对于分类问题,我们建立逻辑回归模型。
针对逻辑回归模型,主要围绕以下几点来讨论。
-
Sigmoid Function (逻辑函数)
-
Decision Boundaries (决策边界)
-
Cost Function (代价函数)
-
One vs All ——逻辑回归在多分类上的应用
Sigmoid Function
首先我们要先介绍一下Sigmoid函数,也称为逻辑函数(Logistic function):
其函数曲线如下:
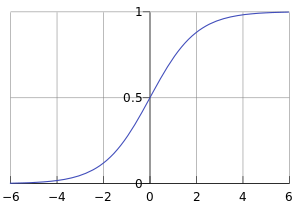
从上图可以看到sigmoid函数是一个s形的曲线,它的取值在[0, 1]之间,在远离0的地方函数的值会很快接近0或者1。它的这个特性对于解决二分类问题十分重要
逻辑回归的假设函数形式如下:
所以:
其中 是我们的输入,
为我们要求取的参数。
一个机器学习的模型,实际上是把决策函数限定在某一组条件下,这组限定条件就决定了模型的假设空间。当然,我们还希望这组限定条件简单而合理。而逻辑回归模型所做的假设是:
这个函数的意思就是在给定 和
的条件下
的概率。
这里 就是我们上面提到的sigmoid函数,与之相对应的决策函数为:
选择0.5作为阈值是一个一般的做法,实际应用时特定的情况可以选择不同阈值,如果对正例的判别准确性要求高,可以选择阈值大一些,对正例的召回要求高,则可以选择阈值小一些。
Decision Boundaries
决策边界不是数据集的属性,而是假设本身及其参数的属性。我们不是用训练集来定义的决策边界,我们用训练集来拟合参数θ,一旦有了参数θ就可以确定决策边界。
决策边界其实就是一个方程,在逻辑回归中,决策边界由 定义。
Cost Function
假设有训练样本 ,模型为
, 参数为
。
(
表示
的转置)。
<1>. 概况来讲,任何能够衡量模型预测出来的值 与真实值
之间的差异的函数都可以叫做代价函数
,如果有多个样本,则可以将所有代价函数的取值求均值,记做
。因此很容易就可以得出以下关于代价函数的性质:
- 选择代价函数时,最好挑选对参数
可微的函数(全微分存在,偏导数一定存在)
- 对于每种算法来说,代价函数不是唯一的;
- 代价函数是参数
的函数;
- 总的代价函数
可以用来评价模型的好坏,代价函数越小说明模型和参数越符合训练样本
;
是一个标量;
<2>. 当确定了模型 ,后面做的所有事情就是训练模型的参数
。那么什么时候模型的训练才能结束呢?这时候也涉及到代价函数,由于代价函数是用来衡量模型好坏的,我们的目标当然是得到最好的模型(也就是最符合训练样本的模型)。因此训练参数的过程就是不断改变
,从而得到更小的
的过程。理想情况下,当我们取到代价函数J的最小值时,就得到了最优的参数
,记为:
例如, ,表示模型完美的拟合了观察的数据,没有任何误差。
<3>. 在优化参数θ的过程中,最常用的方法是梯度下降,这里的梯度就是代价函数 对
的偏导数。由于需要求偏导,我们可以得到另一个关于代价函数的性质:
选择代价函数时,最好挑选对参数 可微的函数(全微分存在,偏导数一定存在)
代价函数的常见形式:
<1>. 在线性回归中,最常用的是均方误差(Mean squared error),即
:训练样本的个数;
:用参数
和
预测出来的y值;
:原训练样本中的
值,也就是标准答案;
- 上角标
:第
个样本。
<2>. 在逻辑回归中,最常用的是代价函数是交叉熵(Cross Entropy),交叉熵是一个常见的代价函数.
One vs All
假设我们要解决一个分类问题,该分类问题有三个类别,分别用△,□和×表示,每个实例(Entity)有两个属性(Attribute),如果把属性 1 作为 X 轴,属性 2 作为 Y 轴,训练集(Training Dataset)的分布可以表示为下图:
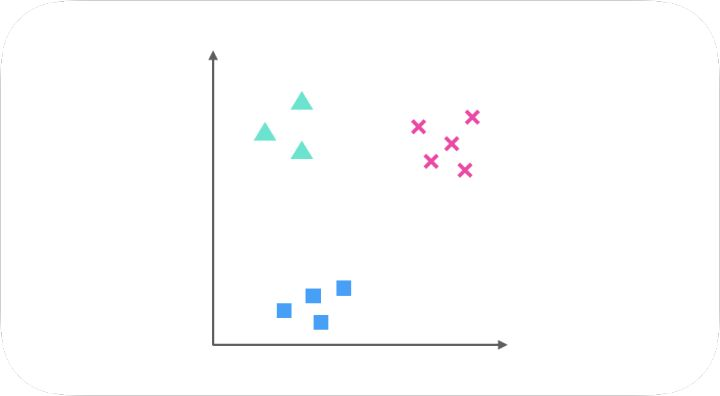
One-Vs-All(或者叫 One-Vs-Rest)的思想是把一个多分类的问题变成多个二分类的问题。转变的思路就如同方法名称描述的那样,选择其中一个类别为正类(Positive),使其他所有类别为负类(Negative)。比如第一步,我们可以将三角形所代表的实例全部视为正类,其他实例全部视为负类,得到的分类器如图:
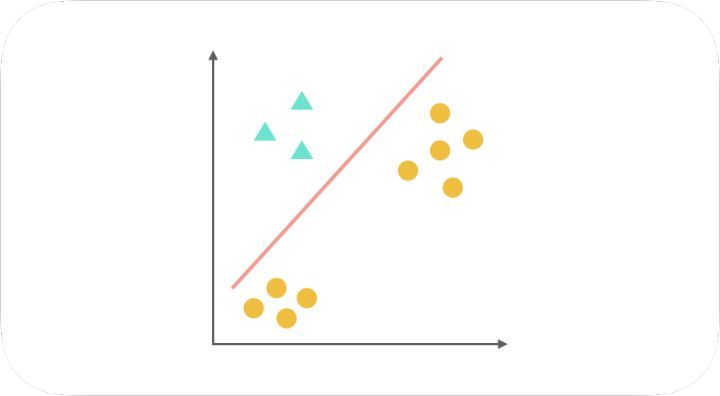
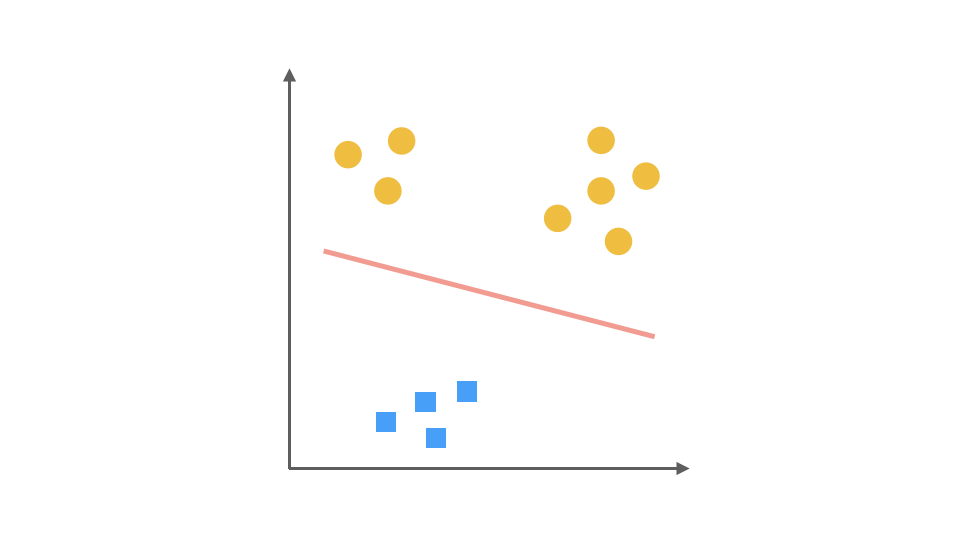
同理我们把 X 视为正类,其他视为负类,可以得到第二个分类器:
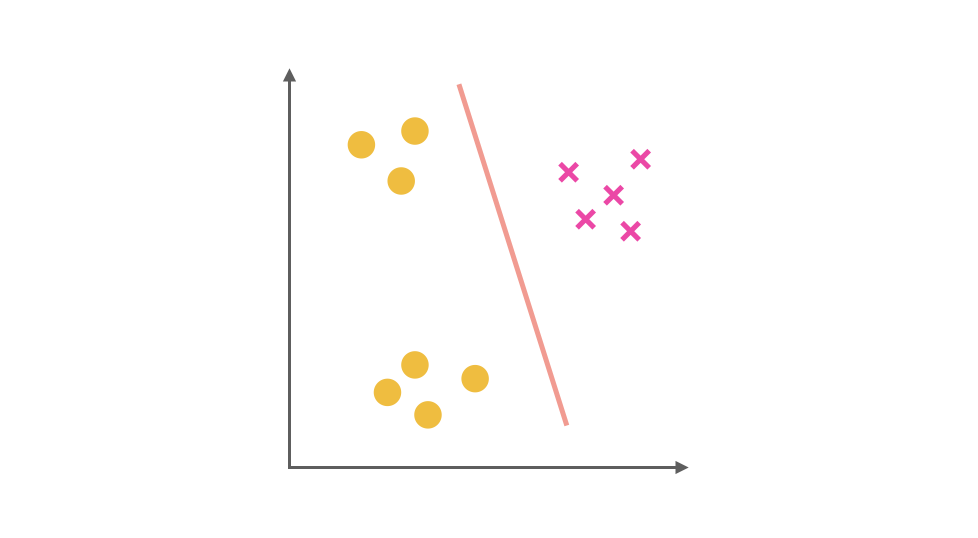
最后,第三个分类器是把正方形视为正类,其余视为负类:
对于一个三分类问题,我们最终得到 3 个二元分类器。在预测阶段,每个分类器可以根据测试样本,得到当前正类的概率。即 P(y = i | x; θ),i = 1, 2, 3。选择计算结果最高的分类器,其正类就可以作为预测结果。
One-Vs-All 最为一种常用的二分类拓展方法,其优缺点也十分明显。
优点:普适性还比较广,可以应用于能输出值或者概率的分类器,同时效率相对较好,有多少个类别就训练多少个分类器。
缺点:很容易造成训练集样本数量的不平衡(Unbalance),尤其在类别较多的情况下,经常容易出现正类样本的数量远远不及负类样本的数量,这样就会造成分类器的偏向性。