支持向量机

支持向量机（Support Vector machine, SVM)，本章节说明如何构建SVM的最优化模型-最优间隔分类器。首先先引入两个间隔定义来衡量预测的置信度。

1. 函数间隔

　　引入函数间隔来描述预测的可靠性。我们从现在开始，本考虑二元分类时，输出值的可取值{-1,1}。

　　当w^Tx+b ≥ 0时，输出类别是1；

　　当w^Tx+b < 0时，输出类别是-1。

函数间隔的定义为：

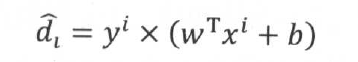
如果训练数据是线性可分的，那么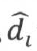恒为非负数，当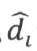值越大，若yⁱ=1，则w^Tx+b ≥ 0，越确信数据属于类别1；若yⁱ=-1，则w^Tx+b ≤ 0，越确定数据属于类别-1。函数间隔能很好地反映出预测的结果置信度。

　　离超平面越近的点对模型的鲁棒性要求越高。（ps：鲁棒性：也就是健壮和强壮的意思。 它是在异常和危险情况下生存的关键）因此，通常关心的是那些离超平面最近的点，这些边界点被称为支持向量（或支撑向量，support vector）。

 

支持向量到超平面的距离是数据集到超平面的最短距离，形式化定义为：

总结：使用函数间隔来衡量预测的置信度有一个不足的地方，那就是当等比例同时方法w和b时，超平面的位置实际上并没有任务变化，而且带你到超平面的距离也没有变化，但函数间隔却变大了。

　

2. 几何间隔

　　为了克服函数间隔的缺点，引入了几何间隔的定义：

从上式可以看出，几何间隔实际上就是点到超平面的欧式距离

 

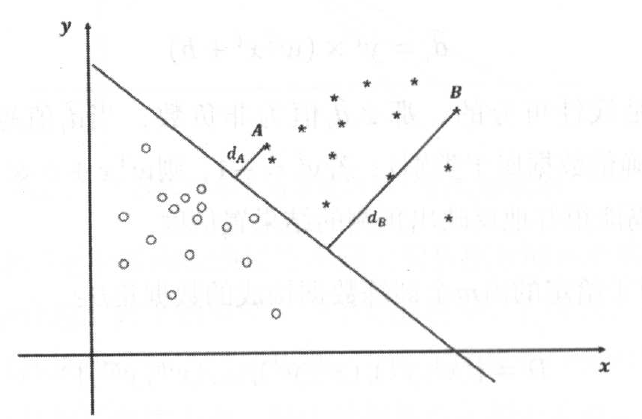
几何间隔的意义与函数间隔一样，当几何间隔越大，其预测结果越可靠。图中的A和B两点，显然B属于类别1的概率要远远大于点A。

与函数间隔一样，重点关注支持向量的几何间隔，定义为：

 

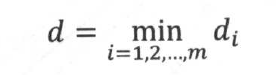
我们的目标是希望间隔越大越好，尤其是我们希望那些边界点，即支持向量的间隔离超平面越大越好。（ps：希望得到的间隔最小值d也是最大化几何间隔后的最小值）为此，得到了下面的带约束的最优化问题：

 

 但由于约束条件||w||=1非凸不可导，先将目标函数从函数间隔的最大值过渡到几何间隔的最大值。

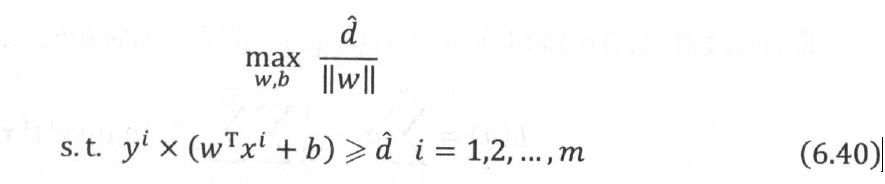
我们总可以将支持向量到超平面的函数间隔值设置为1,也就是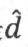=1，同时，通过将最大化问题转化为求最小化问题，是的目标函数变成一个二次的凸函数，凸函数的最优化问题远比非凸函数简单，且能保证获得最优解。因此，转化得到下面的约束最优化问题：

上式就是要求解的SVM最优化模型，由其最优解得到的分类器，称为最优间隔分类器，同时上式也被称为SVM最优化的基本型。

补充：

上式通过最优化策略已经可以求解出最优值，我们还是需要考虑其对偶问题（ps：需要使用拉格朗日乘子法和KKT条件。高效的求解算法是著名的Sequential minimal optimization算法，SMO）。主要基于两方面考虑：

　　一、对偶问题的求解比直接求解原始问题的效率更高；

　　二、对偶问题能更方便引入核函数。

为什么引入核函数？

　　一般情况下，都是假设数据是线性可分的，但在实际应用中，遇到更多的是线性不可分的数据，核函数的作用是用过将线性不可分的输入特征向量映射到高维空间中，使得映射后的结果在高维空间能够用过超平面分离。

 

几个常见的核函数：

1. 多项式核

2. 高斯核