计算几何小结1

部分内容摘自http://blog.csdn.net/clover_hxy/article/details/53966405

一、精度控制

计算几何经常牵扯到浮点数的运算，所以就会产生精度误差，因此我们需要设置一个eps（偏差值），一般取1e-10之间，并用下面的函数控制精度

#define eps (1e-10)
#define equal(a,b) (fabs((a)-(b))) < eps

加上括号增加容错性

二、向量（点，默认表示从0,0点引出得向量）

class Point{
    public:
    double x,y;

    Point(double x = 0,double y = 0):x(x),y(y){}

    Point operator + (Point p){return Point(x + p.x,y + p.y);}
    Point operator - (Point p){return Point(x - p.x,y - p.y);}
    Point operator * (double a){return Point(a * x,a * y);}
    Point operator / (double a){return Point(x / a,y / a);}

    double abs(){return sqrt(norm());}
    double norm(){return x * x + y * y;}
    bool operator < (const Point &p) const
    {
        return x != p.x ? x < p.x : y < p.y;
    }

    bool operator == (const Point &p) const
    {
        return fabs(x - p.x) < eps && fabs(y - p.y) < eps;
    }
};

用结构体定义也没有区别，特地查了一下：

在C++ 语言中class是定义类的关键字，C++中也可以使用struct定义类。
两者区别是，用class定义的类，如果数据成员或成员函数没有说明则默认为private（私有）的，而用struct定义的默认为public（公共）的。
 public修饰：公有成员，基类、子类、友元、外部都可以访问
 private修饰：私有成员，基类、友元可以访问，子类、外部不可以访问

一个点，有x和y两个坐标，但他的意义并不是一个点而是一个OP向量，只不过O是（0，0）,所以对于向量我们定义了四则运算

Point operator + (Point p){return Point(x + p.x,y + p.y);}
    Point operator - (Point p){return Point(x - p.x,y - p.y);}
    Point operator * (double a){return Point(a * x,a * y);}
    Point operator / (double a){return Point(x / a,y / a);}

然后是向量得膜（大小）和大小的平方，称为范数(P.abs())（当然也可以定义在外面，用的时候是abs(P);）

double abs(){return sqrt(norm());}//大小
double norm(){return x * x + y * y;}//范数

定义了两个比较运算符

bool operator < (const Point &p) const
    {
        return x != p.x ? x < p.x : y < p.y;
    }

    bool operator == (const Point &p) const
    {
        return fabs(x - p.x) < eps && fabs(y - p.y) < eps;
    }

这时候一个点（向量就定义好了）可以开始定义线段（直线了）它们由两个点组成

struct Segment {
    Point p1,p2;
};

也可以定义多边形，他们是点的序列：

typedef vector<Point> Polygon;//点的序列

三、内积（点积）

 向量a,b得夹角为A,其内积就是

a·b=|a||b|cosθ,其中θ为a,b之间的夹角，化简开来

double dot(Point a,Point b){return a.x * b.x + a.y * b.y;}//内积

应用：

1.判断两个向量是否正交（垂直）

两个向量垂直，向量可以自由挪动，挪到一个公共点上，那么特们之间得夹角是90度和-90度，所以内积为0(可以传值两个点，四个点，两个线段（直线）都是等价得)

//正交判断
bool isOrthogonal(Point a,Point b)
{
    return equal(dot(a,b),0.0);
}
bool isOrthogonal(Point a1,Point a2,Point b1,Point b2)
{
    return isOrthogonal(a1 - a2,b1 - b2);
}
bool isOrthogonal(Segment s1,Segment s2)
{
    return equal(dot(s1.p2 - s1.p1,s2.p2 - s2.p1),0.0);
}

2.求夹角

double Angle(Point a,Point b)
{
    return acos(dot(a,b)/a.abs()/b.abs());
}

3.求投影坐标/长度

求p点在向量p1p2上的投影点得坐标

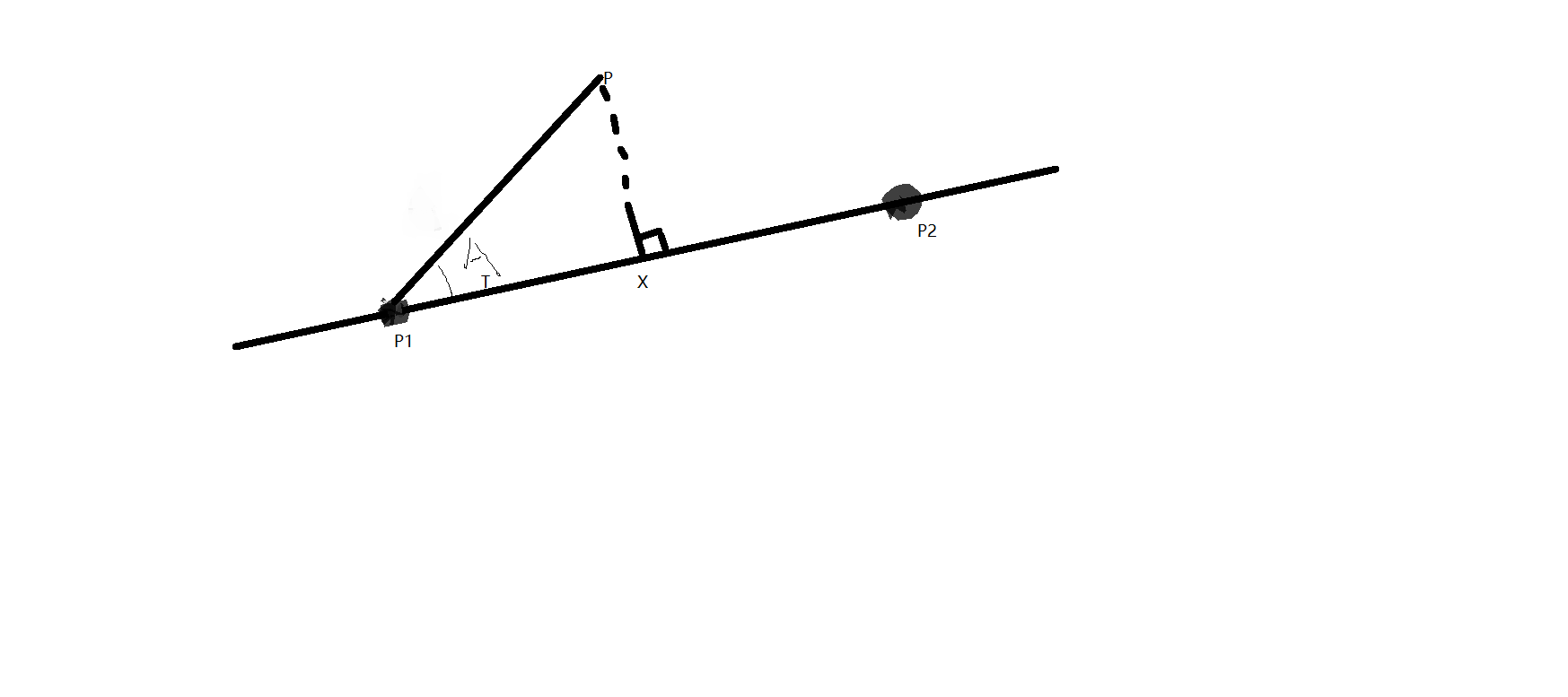
令base向量表示p1p2，heap向量表示p1p,投影点为x，p1x.abs() = t

夹角是A，那么t = heap.abs() * cosA heap * base（内积）得出t,t = 内积 / base.abs(),现在有了t得大小，base得大小，又知道p1得坐标，还差的就是t和base得比例r = t / base.abs(),所以r = t / base.norm(),x得坐标就是p1 + base * r

//投影坐标
Point project(Segment s,Point p)
{
    Point base = s.p2 - s.p1;
    Point heap = p - s.p1;
    double r = dot(heap,base) / base.norm();
    return s.p1 + base * r;
}

知道了投影坐标经过一系列变化，我们还能得到对称点的坐标

Point reflet(Segment s,Point p)
{
    return p + (project(s,p) - p) * 2.0;
}

 就是向量op + pp' = op'

Ps插播一个法向量，是我没了解过的

Point normal(Point a)
{ 
    double l=a.abs();
    return Point (-a.y/l,a.x/l);
}

四、外积（叉积）

 两个向量得外积是一个具有大小和方向的向量，方向判断：方向与，a,b所在的平面垂直，规定好向量a,b的共同端点o,那么oa转到ob如果是顺时针那么外积方向为正（向上，oa,ob夹角为A）反之向下(oa，ob夹角为-A)（右手定则）

a * b (叉积) = a.abs() * b.abs() * sinA（也能表示出外积的方向问题）化简后：

double cross(Point a,Point b){return a.x * b.y - a.y * b.x;}//外积

 也三个参数的（）

double cross(Point p1, Point p2,Point p3)
{
    Point a = p2 - p1;
    Point b = p3 - p1;
    return cross(a,b);
}

 另一种理解方式

直观理解，假如b在a的左边，则有向面积为正，假如在右边则为负。假如b,a共线，则叉积为0,。

所以叉积可以用来判断平行。

Ps插播一个向量旋转

 向量的旋转

a=(x,y)可以看成是x*(1,0)+y1*(0,1)

分别旋转两个单位向量，则变成x*(cosθ，sinθ)+y1*(-sinθ，cosθ)

 应用：

1.用于判断两向量是否平行也就是根据sin的性质来的

bool isParallel(Point a,Point b)
{
    return equal(cross(a,b),0.0);
}
bool isParallel(Point a1,Point a2,Point b1,Point b2)
{
    return isParallel(a2 - a1,b2 - b1);
}
bool isParallel(Segment s1,Segment s2)
{
    return equal(cross(s1.p2 - s1.p1,s2.p2 - s2.p1),0.0);
}

2.点到直线的距离

就是到垂线的长度

double getDistanceLP(Segment l,Point p)
{
    return cross(l.p2 - l.p1,p - l.p1) / (l.p2 - l.p1).abs();
}

 求p1p2 和 p1p的叉积就是求以他俩为临边的平行四边形的面子除以一边就得到了高

3.点到线段的距离

和直线不同 ，主要是对于线段，点可能在线段范围外，无法投影

double getDistanceSP(Segment s,Point p)
{
    if(dot(s.p2 - s.p1,p - s.p1) < 0.0)return (p - s.p1).abs();
    if(dot(s.p2 - s.p1,p - s.p2) < 0.0)return (p - s.p2).abs();
    return getDistanceLP(s,p);
}

 用内积判断夹角，如果小于零则代表出了范围

4.综合利用

static const int COUNTER_CLOCKWISE = 1;//在逆时针方向
static const int CLOCKWISE = -1;//顺时针方向
static const int ONLINE_BACK = 2;//p2 p0 p1
static const int ONLINE_FRONT = -2;//p0 p1 p2
static const int ON_SEGMENT = 0;//p0 p2 p1
int ccw(Point p0,Point p1,Point p2)
{
    Point a = p1 - p0;
    Point b = p2 - p0;
    if(cross(a,b) > eps)return COUNTER_CLOCKWISE;
    if(cross(a,b) < -eps)return CLOCKWISE;
    if(dot(a,b) < -eps)return ONLINE_BACK;
    if(a.norm() < b.norm())return ONLINE_FRONT;
    return ON_SEGMENT;
}

 先用外积判断点在线的顺时针还是逆时针，如果在线上并且内积 < 0就代表在线外（夹角为180）

在判断长度就可以得到比较具体的位置关系

5.以ccw为基础可以进行线段相交的判断了

对于两个线段如果双方都符合另一条线段的两个端点分别在这条线段的两个方向，那就会相交（如果是直线和线段的话只要一方符合就ok，直线直线的话，不平行就相交，对了注意重合的考虑）

bool intersect(Point p1,Point p2,Point p3,Point p4)
{
    return (ccw(p1,p2,p3) * ccw(p1,p2,p4) <= 0 && ccw(p3,p4,p1) * ccw(p3,p4,p2) <= 0 );
}
bool intersect(Segment s1,Segment s2)
{
    return (ccw(s1.p1,s1.p2,s2.p1) * ccw(s1.p1,s1.p2,s2.p2) <= 0 && ccw(s2.p1,s2.p2,s1.p1) * ccw(s2.p1,s2.p2,s1.p2) <= 0 );
}

6.以5.0为基础就能求线段到线段的距离了

 如果线段相交，距离为0，否则就是找各个端点到另一条线段的距离，转化为点到线段的距离了

double getDistanceSS(Segment s1,Segment s2)
{
    if(intersect(s1,s2))return 0.0;
    return min(min(getDistanceSP(s1,s2.p1),getDistanceSP(s1,s2.p2)),
               min(getDistanceSP(s2,s1.p1),getDistanceSP(s2,s1.p2)));
}

 7.求线段的交点

也是一系列的几何操作,设交点为x

 以s2作为基向量，求取s1两个端点到直线s2的距离（利用外积，平行四边形）接下来就是求比例，p1x和p1p2(均指长度)的比列用相似三角形 t = d1 / (d1 + d2)

接下来就是求向量p1x （就是）(s1.p2 - s1.p1) * t

Point getCrossPoint(Segment s1,Segment s2)
{
    Point base = s2.p2 - s2.p1;
    double d1 = abs(cross(base,s1.p1 - s2.p1));
    double d2 = abs(cross(base,s1.p2 - s2.p1));
    double t = d1 / (d1 + d2);
    return s1.p1 + (s1.p2 - s1.p1) * t;
}

 先小结到这儿吧，太多了估计我以后也没兴趣看了~~