Dinic是很好的算法,但是我还是从ek算法复习起步
面对最大流问题,印象最深的就是反向边的思想,他给我们提供了反悔的机会,其实现在放到实际上来想,可以相当于两边的水都流了这条边,只是方向不一样,放到程序上,就是添加反向边。
ek算法是基础的算法,思想也比较简单,就是先用bfs去寻找一波可行的1 到 n 的最大流,然后记录每一个经过的结点的前驱,在调用ek算法建立反向边,时间上面也是很费时,所以才有必要去学习Dinic算法及其优化的版本,这里就不粘贴我的ek算法的代码了……
果然是温故而知新,复习了一晚上Dinic算法,有对他有了新的理解和认识,相对于ek算法,dinic算法的优化真的是非常的好——当前弧优化
#include <iostream>
#include <string.h>
#include <cstdio>
#include <queue>
#define inf 0xfffffff
using namespace std;
const int maxn = 220;//最大的结点数量
const int maxm = 4e4 + 4e2;//边的数量
int n,m;
struct node{
int pre;
int to,cost;
}e[maxm];
int id[maxn],cnt;
int flor[maxn];
void init()
{
memset(id,-1,sizeof(id));
cnt = 0;
}
int cur[maxn];
void add(int from,int to,int cost)
{
e[cnt].to = to;
e[cnt].cost = cost;
e[cnt].pre = id[from];
id[from] = cnt++;
swap(from,to);
e[cnt].to = to;
e[cnt].cost = 0;
e[cnt].pre = id[from];
id[from] = cnt++;
}
上面都是基本的存储结构,链式前向星存储,反向边的建立,层数的记录
先面整体观看一下Dinic算法
int Dinic(int s,int t)
{
int ret = 0;
while(bfs(s,t))//进行分层预处理
{
for(int i = 1;i <= n;i++)
{
cur[i] = id[i];
}
ret += dfs(s,t,inf);//dfs寻找最大增广路
}
return ret;
}
bfs进行分层处理,dfs进行最大增广路的寻找,cur数组时dfs中优化的一个关键,后面会提及
先来看看bfs分层处理
int bfs(int s,int t)
{
queue<int>q;
while(q.size())q.pop();
memset(flor,0,sizeof(flor));
flor[s] = 1;
q.push(s);
while(q.size())
{
int now = q.front();
q.pop();
for(int i = id[now];~i;i = e[i].pre)
{
int to = e[i].to;
int cost = e[i].cost;
if(flor[to] == 0/*冲当了vis*/ && cost > 0/*还有流量*/ )
{
flor[to] = flor[now] + 1;
q.push(to);
if(to == t)return 1;//分层到终点结束立即返回
}
}
}
return 0;
}
根据边的关系flor数组还充当vis数组,进行层级标记,为后续的dfs做准备,bfs何时返回呢要么时到了中点返回1,要么是到不了终点返回0
精彩的时dfs,当前弧的优化思想太厉害太厉害了
int dfs(int s,int t,int value)//起点,终点,当前流量
{
//寻找增广路
int ret = value;
if(s == t || value == 0)return value;//要么是路通了,要么是没路了
int a;
//找不到t了,因为到t的边流量都变成了0!!
/*
优化的时候记录优化到哪条边了
所以对于每一条边我只会访问一次
*/
for(int &i = cur[s];~i;i = e[i].pre)
{
int to = e[i].to;
if(flor[to] == flor[s] + 1 && (a = dfs(to,t,min(ret,e[i].cost))))
{
e[i].cost -= a;//对于这条边的优化操作
e[i^1].cost += a;
ret -= a;//最后返回的是ret -= a 所以我们是记录了a的
if(!ret)break;//ret == 0时
/*
ret记录了s到to的最大流量值a呢是to到t的最大流量
当ret - a == 0 的时候就可以结束了,往前返回的是value值,进行后续边的优化
*/
/*
为什么不相等的时候不会退出呢??
不相等,也就是ret > a,这是后前面的路都至少还有ret - a的残量,可以继续dfs进行优化更新
*/
}
}
if(ret == value)flor[s] = 0;//中间结点遍历了所有的边,得到的结果是无路(流量),所以标志中间结点s废掉
return value - ret;
}
先来放一张我画的惨图
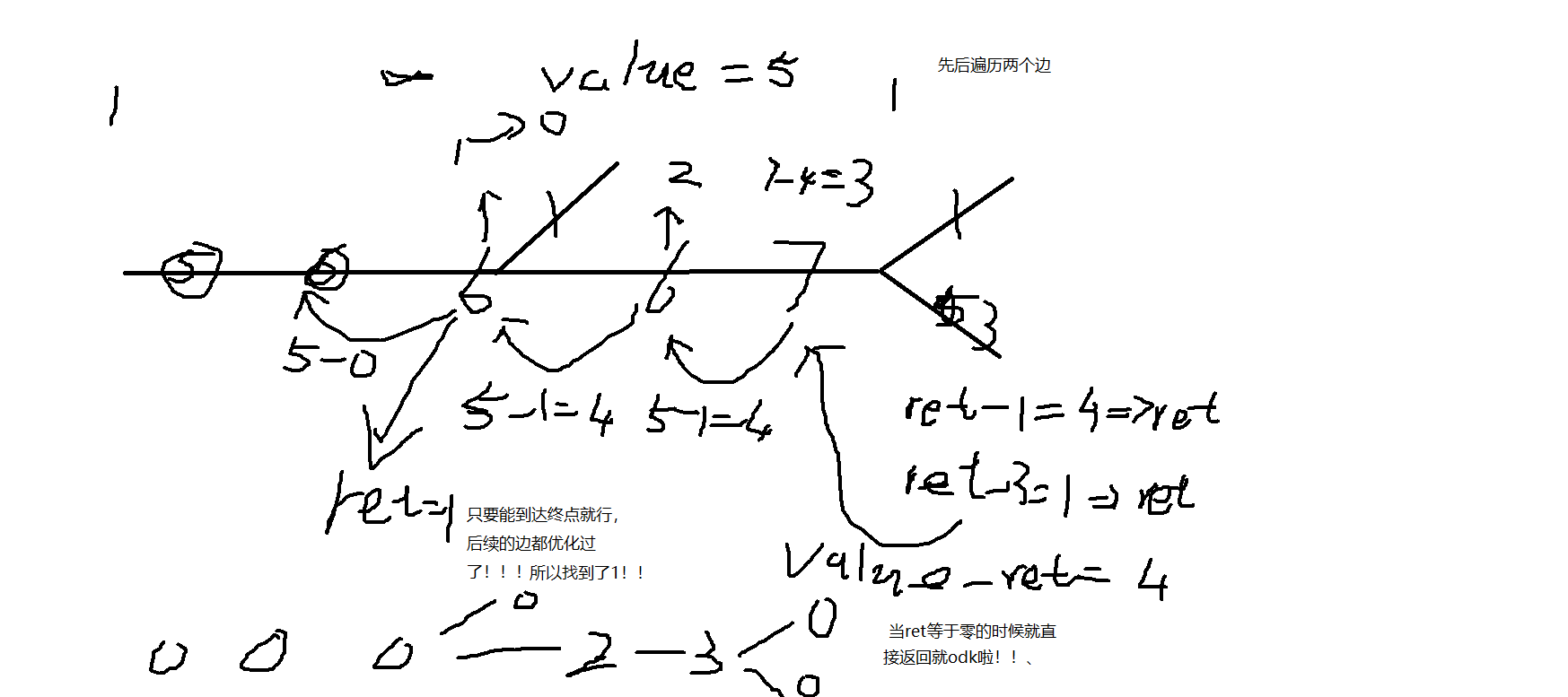
没错,一开始我对初始传参dfs(s,t,inf)传入inf不是太理解,第一次调用什么都没有连同,所以可流量时无限大的,也为了结下的递归做了铺垫
然后dfs的递归设置结束的条件1.找到了2.当前可流量变成了零也就没必要继续找了不是??
当前弧优化的经典就是cur数组,也就是id数组的副本,记录了边的信息,C++的引用确保了对于这个点的边信息我只会dfs一次,不会重复dfs这样就大大的节约了时间
然后a接受的时to 到 t 的最大流量,返回之后层层进行边和反向边的更新ret -= a时什么意思呢??首先来看看ret表示的什么吧递归进来的时候ret和value都表示的时s 到 to的最大可流量,而a表示的时to 到 t 的最大流量,我们要对to前面的边进行优化,所以ret -= a表示的时s 到 to的那些点还有没有可流能力如果ret = 0那就不可再流直接返回,反之可以再留,就继续根据cur数组进行后面边的查询,直到查询结束,跳出的时候你可以判断一下如果当前s点后没有一条就可以标记s点为费点接下来的dfs回溯优化不会在考虑s点了,也是一个小小的优化吧
到此,Dinic算法就告于段落了~~
——————————————————————————————————————————————————
加油!!