https://codeforces.ml/contest/1333/problem/C
大概题意是规定和为0的数组为不合格数组,询问给定数组中共有多少个合格子数组。
解题
子数组的数量
一个长度为 (n) 的数组 (a[0,n-1]),选取 (i) 作为子数组的终点,那么我们可以选取 ([0,i]) 中的任何一个 (j) 作为起点,这样可以得到子数组 (a[j,i]) ,所以以 (i) 为终点的子数组有 (i+1) 种。以此类推,最终子数组的总个数为 (count=sum_{i=0}^{n-1}(i+1)= (n+1)*n/2) 。
合格子数组的数量
根据题意可得,如果一个数组是不合格的(存在子数组和为0),则含有这个数组的所有父亲数组都是不合格的。
当我们以 (i) 为子数组终点时。
如果子数组 (a[p_1,p_2](p_2le i)) 是不合格数组,那么我们只能在 ((p_1,i]) 区间内选取起点 (j) (共 (i-p_1) 种),否者新数组会成为不合格部分的父亲数组。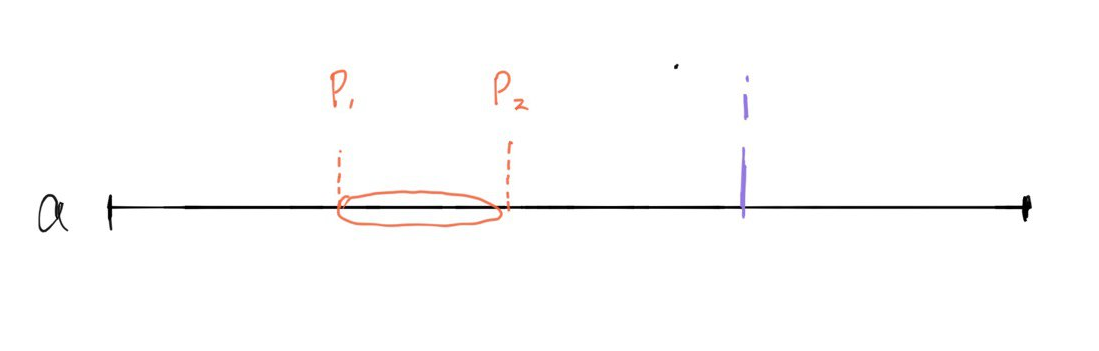
如果 (p_2 gt i) 的话,则可以在 ([0,i]) 区间内选取起点 (j),共计 (i+1) 种。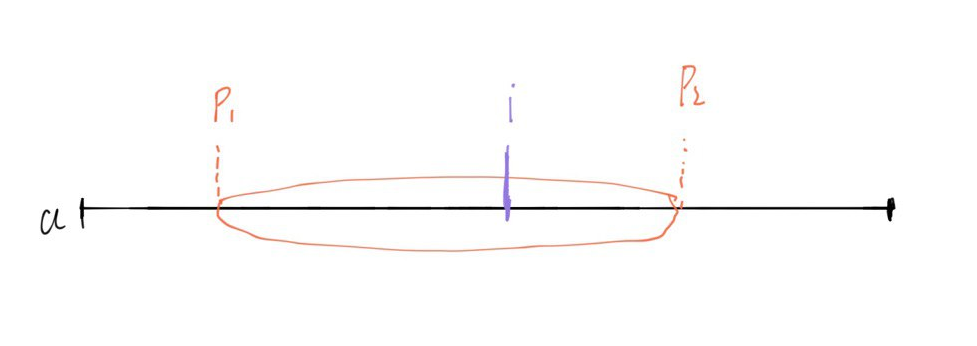
我们设 (s) 为所有出现在位置 (i) 之前的不合格子数组的起点位置的集合。设 (f(i)) 为以 (a_i) 为结尾的合格子数组个数,(f(i) = i-max{p|p<i,pin s}),如果 (p) 不存在,那么 (f(i) = i+1)。
全部合格子数组的数量 (ans = sum_{all}f(i)),不会重复计算。
代码
#include<bits/stdc++.h>
#define ll long long
#define fr(i,n) for(int i=0;i<n;i++)
#define frs(i,n,flag) for(int i=0;i<n&&flag;i++)
#define frr(i,j,n) for(int i=j;i<n;i++)
#define r_frr(i,j,n) for(int i=n-1;i>=j;i--)
#define frrs(i,j,n,flag) for(int i=j;i<n&&flag;i++)
#define r_frrs(i,j,n,flag) for(int i=n-1;i>=j&&flag;i--)
#define arend(i,n) ((i!=n-1)?" ":"
")
#define memset0(dp) memset(dp,0,sizeof(dp))
#define print_arr(begin,end) for(auto it = begin;it!=end;it++) cout<<*it<<arend(it,end);
#define log_this(name,value) cout<<name<<": "<<value<<endl;
#define e4 10004#define e5 100005#define e6 1000006#define e7 10000007#define e9 1000000000#define INF 9999999
using namespace std;
int to_int(string s) {stringstream ss;ss<<s;int a;ss>>a;return a;}
string to_str(double a) {stringstream ss;ss<<a;return ss.str();}
int main(){
cin.tie(0);
//ios::sync_with_stdio(false);
//cout<<setiosflags(ios::fixed)<<setprecision(0);
//freopen("1.out","w",stdout);
int n;
while(cin>>n){
ll sum=0,p=-1,ans=0,inp;
map<ll,ll>loc;loc[0] = 0;
fr(i,n){
cin>>inp;
sum += inp;
auto it = loc.find(sum);
if(it!=loc.end()){
p = max(p,loc[sum]);
}
loc[sum] = i+1;
ans += i - p;
}
cout<<ans<<endl;
}
return 0;
}