Codeforces Round #385 (Div. 2) Hongcow Builds A Nation —— 图论计数

题目链接：http://codeforces.com/contest/745/problem/C

C. Hongcow Builds A Nation

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Hongcow is ruler of the world. As ruler of the world, he wants to make it easier for people to travel by road within their own countries.

The world can be modeled as an undirected graph with n nodes and m edges. k of the nodes are home to the governments of the kcountries that make up the world.

There is at most one edge connecting any two nodes and no edge connects a node to itself. Furthermore, for any two nodes corresponding to governments, there is no path between those two nodes. Any graph that satisfies all of these conditions is stable.

Hongcow wants to add as many edges as possible to the graph while keeping it stable. Determine the maximum number of edges Hongcow can add.

Input

The first line of input will contain three integers n, m and k (1 ≤ n ≤ 1 000, 0 ≤ m ≤ 100 000, 1 ≤ k ≤ n) — the number of vertices and edges in the graph, and the number of vertices that are homes of the government.

The next line of input will contain k integers c1, c2, ..., ck (1 ≤ ci ≤ n). These integers will be pairwise distinct and denote the nodes that are home to the governments in this world.

The following m lines of input will contain two integers ui and vi (1 ≤ ui, vi ≤ n). This denotes an undirected edge between nodes ui and vi.

It is guaranteed that the graph described by the input is stable.

Output

Output a single integer, the maximum number of edges Hongcow can add to the graph while keeping it stable.

Examples

input

4 1 2
1 3
1 2

output

2

input

3 3 1
2
1 2
1 3
2 3

output

0

Note

For the first sample test, the graph looks like this:

Vertices 1 and 3 are special. The optimal solution is to connect vertex 4 to vertices 1 and 2. This adds a total of 2 edges. We cannot add any more edges, since vertices 1 and 3 cannot have any path between them.

For the second sample test, the graph looks like this:

We cannot add any more edges to this graph. Note that we are not allowed to add self-loops, and the graph must be simple.

题意：

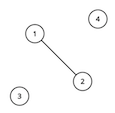
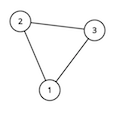
给出一张无向图，图中有k个点为特殊点，且图满足：每对特殊点直接没有通路。问：最多能添加多少条边，使得图仍能满足上述条件？

题解：

1.将每个连通块缩成一个集合，这个集合需要记录的信息有：点的个数，以及是否含有特殊点（最多有1个）。

2.根据集合中点的个数，将集合降序排序。

3.首先计算出一个集合内的所有边（完全图），即：num*（num-1）/2；然后挑选点数最大的两个集合，如果这两个集合最多只有一个特殊点，那么意味着他们可以合并，于是合并，共添加了num1*num2条边。

4.由于步骤3计算的是添加边后，总的边数，所以减去初始图的边数，才为添加的边数。

代码如下：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <string>
#include <set>
using namespace std;
typedef long long LL;
const int INF = 2e9;
const LL LNF = 9e18;
const int mod = 1e9+7;
const int MAXM = 1e6+10;
const int MAXN = 1e4+10;

struct Node
{
    bool hav;
    int num;
    bool operator<(const Node &x)const{
        return num>x.num;
    }
}q[MAXN];

vector<int>g[MAXN];
bool isgov[MAXN], vis[MAXN];

void dfs(int u, int index)
{
    vis[u] = true;
    q[index].num++;
    if(isgov[u]) q[index].hav = true;
    for(int i = 0; i<g[u].size(); i++)
        if(!vis[g[u][i]])
            dfs(g[u][i], index);
}

int main()
{
    int n, m, k;
    scanf("%d%d%d", &n,&m,&k);
    memset(isgov, false, sizeof(isgov));
    for(int i = 1; i<=n; i++) g[i].clear();
    for(int i = 1; i<=k; i++)
    {
        int u;
        scanf("%d", &u);
        isgov[u] = true;
    }
    for(int i = 1; i<=m; i++)
    {
        int u, v;
        scanf("%d%d", &u,&v);
        g[u].push_back(v);
        g[v].push_back(u);
    }

    int index = 0;
    memset(q, 0,sizeof(q));
    memset(vis, false, sizeof(vis));
    for(int i = 1; i<=n; i++)
        if(!vis[i])
            dfs(i, ++index);

    sort(q+1,q+1+index);
    int ans = (q[1].num-1)*q[1].num/2;
    for(int i = 2; i<=index; i++)
    {
        ans += (q[i].num-1)*q[i].num/2;
        if(!q[1].hav || !q[i].hav)
        {
            ans += q[1].num*q[i].num;
            q[1].num += q[i].num;
            q[1].hav = q[1].hav||q[i].hav;
        }
    }

    ans -= m;
    printf("%d
", ans);
}