主要内容：
一.损失函数
二.决策边界
三.Kernel
四.使用SVM
（有关SVM数学解释：机器学习笔记（八）震惊！支持向量机（SVM）居然是这种机）
一.损失函数
二.决策边界
对于：
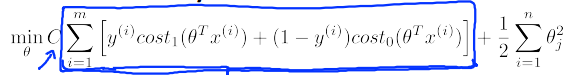
当C非常大时，括号括起来的部分就接近于0，所以就变成了：
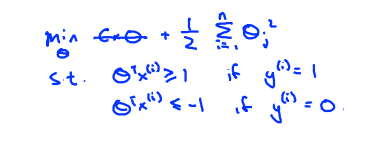
非常有意思的是，在最小化 1/2*∑θj^2的时候，最小间距也达到最大。原因如下：
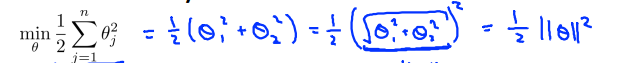
所以：
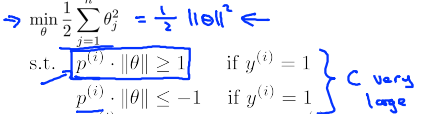
即：如果我们要最小化1/2*∑θj^2，就要使得||θ||尽量小，而当||θ||最小时，又因为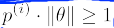
，所以p(i)最大，即间距最大。
注意：C可以看成是正则项系数λ的倒数。所以，当C越大时（可以看成是λ越小），则曲线对于数据越敏感。如下：
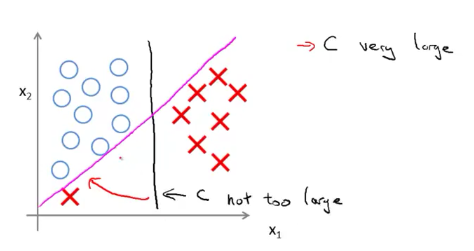
三.Kernel
上面介绍的都是线性可分的情况，当线性不可分时，或许我们可以用多项式进行拟合，如下：
但是多项式的次数太高，计算成本就会很大，有没有更好的办法？那就是SVM带核的方法。
我们将上面的多项式改为：
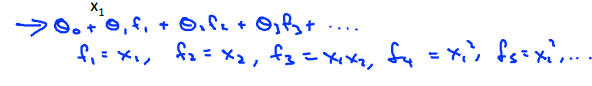
然后f的公式为：
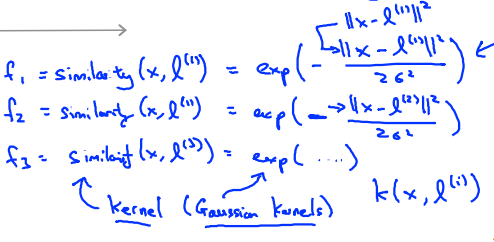
这个f函数就是高斯核函数。
我们在坐标轴上选取三个地标
其中f1就是坐标轴上某一点到L(1)距离的远近，离得近则f1 = 1，离得远则f1 = 0，f2、f3等以此类推。
对于高斯核函数，σ对整体分布的影响为：σ越大，分布越扁平：
于是新的决策方法就变为：
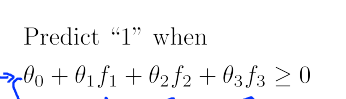
那么如何选取地标L呢？那就是数据集的每一点都作为地标，如下：
综上，带核的SVM可以描述为：
四.使用SVM
支持向量机较为复杂，一般而言，我们都不会自己去实现算法，而是直接调用。但是我们需要做两点工作，那就是：1.选择C的值（cost function上的那个系数C），2.选择核函数（或者直接使用无核），具体步骤如下：
