相关博客:
吴恩达机器学习笔记(八) —— 降维与主成分分析法(PCA)
《机器学习实战》学习笔记第十三章 —— 利用PCA来简化数据
主要内容:
一.SVD简介
二.U、∑、VT三个矩阵的求解
三.U、∑、VT三个矩阵的含义
四.SVD用于PCA降维
五.利用SVD优化推荐系统
六.利用SVD进行数据压缩
一.SVD简介
1.SVD分解能够将任意矩阵着矩阵(m*n)分解成三个矩阵U(m*m)、Σ(m*n)、VT(n*n),如下:
Datamxn = Umxm∑mxnVTnxn
2.Σ是一个对角矩阵,其对角元素是从大到小排列的,它们对应了Data矩阵的奇异值。这些奇异值的含义类似于PCA中特征值的含义。
3.V是一个列矩阵(因而VT是一个行矩阵)、是一个标准正交基,可用于将数据集Data矩阵进行列降维(即减少列数),其作用类似于PCA中的正交矩阵P。
4.U是一个列矩阵、是一个标准正交基,可用于将数据集Data矩阵进行行降维(即减少行数)。
二.U、∑、V三个矩阵的求解及其含义
可知:D = U∑VT
则:DTD = V∑TUTU∑VT = V∑T∑VT = V∑2VT,因为U为正交矩阵,所以UTU = I, 因为∑为对角矩阵,所以∑T∑可表示为∑2。
即:DTD = V∑2VT
可知DTD是一个方阵,方阵即可求出他的特征值和特征向量
(DTD)X = λX
其中∑2就是特征值λ构成的对角矩阵,V就是特征向量X构成的正交矩阵。
因此,可以用求解特征值和特征向量的方法求解矩阵∑、V。同理,通过求解DDT的特征值和特征向量可以求解出矩阵U。
三.U、∑、VT三个矩阵的含义
1.矩阵V的含义:根据上一节,可知矩阵V就是DTD的特征向量组成的正交矩阵,也就是正交基。而在PCA中,正交基P也是DTD的特征向量组成的正交矩阵。即,求解矩阵V实际上是在PAC中求解P。而正交基P正是用于对矩阵D进行列降维(减少列数,即减少属性个数),因此得出结论:矩阵V用于对矩阵D进行列降维。
2.矩阵U的含义:与矩阵V相对,矩阵U用于对矩阵D进行行降维(减少行数,即减少数据点个数)。
3.根据上一节,矩阵∑2就的对角元素就是DTD的特征值,那么矩阵∑的对角元素DTD的特征值的开根。∑的对角元素又称为奇异值。注意:求解U和求解V时∑2是不一样的,一个是m*m,一个是n*n,但它们的对角元素是一样的(min(m,n)个奇异值,缺少的用0表示)。
四.SVD用于PCA降维
1.SVD即奇异值分解,可以用来降维。利用PCA降维不挺好的,什么还要用SVD呢?
因为在使用PCA进行降维时,需要计算协方差矩阵XTX,而如果样本数、特征数都特别多时,计算XTX将非常耗时。但利用SVD,可以不用求出协方差矩阵XTX也能得到用于降维的矩阵。实际上,sklearn的PCA就是用SVD求解的。
2.类似于PCA,如果前k个奇异值所对应包含的信息超过了90%,那么可以只利用前k维进行数据压缩,如下:
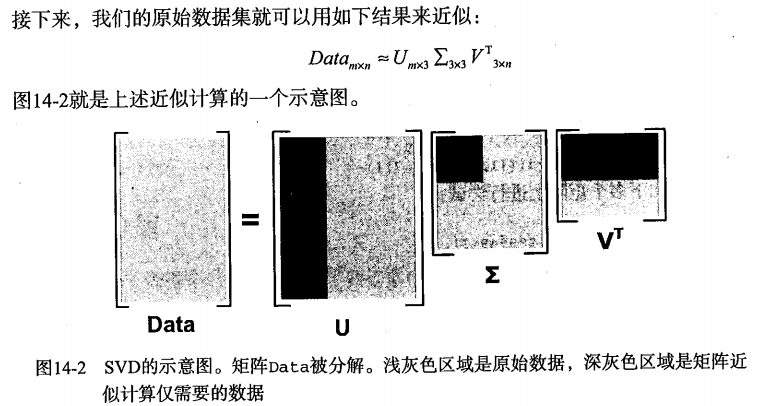
在传输数据时,我们可以只传U(m*k)、Σ(k*k)、VT(k*n)这三个小矩阵。当接受完数据时,就可以将这三个小矩阵进行矩阵乘法,从而得到原始数据集矩阵Data的近似矩阵。这种方式大大压缩了存储(或传输)的数据量,但又保证了高相似度。
2.SVD可用于降维,将求得的U(m*m)矩阵保留前k列,然后将数据集Data映射的U(m*k)上,实现降维。同理矩阵V(m*m)。
五.利用SVD优化推荐系统
1 def ecludSim(inA, inB): # 计算两数组的相似度 2 return 1.0 / (1.0 + la.norm(inA - inB)) 3 4 def pearsSim(inA, inB): # 同上 5 if len(inA) < 3: return 1.0 6 return 0.5 + 0.5 * corrcoef(inA, inB, rowvar=0)[0][1] 7 8 def cosSim(inA, inB): # 同上 9 num = float(inA.T * inB) 10 denom = la.norm(inA) * la.norm(inB) 11 return 0.5 + 0.5 * (num / denom) 12 13 '''对单个物品进行预测评分''' 14 def standEst(dataMat, user, simMeas, item): 15 n = shape(dataMat)[1] # 物品数 16 simTotal = 0.0; ratSimTotal = 0.0 # 总相似度、总评分, 预测频分 = 总评分/总相似度 17 for j in range(n): # 枚举所有物品 18 userRating = dataMat[user, j] # 获取该用户对此物品的评分 19 if userRating == 0: continue # 如果未进行评分,则下一个物品 20 overLap = nonzero(logical_and(dataMat[:, item].A > 0, dataMat[:, j].A > 0))[0] #寻找对两个物品都评了分的用户 21 if len(overLap) == 0: # 计算相似度 22 similarity = 0 23 else: 24 similarity = simMeas(dataMat[overLap, item], dataMat[overLap, j]) 25 print 'the %d and %d similarity is: %f' % (item, j, similarity) 26 simTotal += similarity 27 ratSimTotal += similarity * userRating 28 if simTotal == 0: 29 return 0 30 else: 31 return ratSimTotal / simTotal 32 33 '''对单个物品进行预测评分,利用SVD对用户进行降维''' 34 def svdEst(dataMat, user, simMeas, item): 35 n = shape(dataMat)[1] 36 simTotal = 0.0; ratSimTotal = 0.0 37 U, Sigma, VT = la.svd(dataMat) # 奇异值分解 38 Sig4 = mat(eye(4) * Sigma[:4]) # 取前四个奇异值进行降维 39 xformedItems = dataMat.T * U[:, :4] * Sig4.I # 降维(用户那一栏减少了) 40 for j in range(n): 41 userRating = dataMat[user, j] 42 if userRating == 0 or j == item: continue 43 similarity = simMeas(xformedItems[item, :].T, xformedItems[j, :].T) 44 print 'the %d and %d similarity is: %f' % (item, j, similarity) 45 simTotal += similarity 46 ratSimTotal += similarity * userRating 47 if simTotal == 0: 48 return 0 49 else: 50 return ratSimTotal / simTotal 51 52 '''推荐算法''' 53 def recommend(dataMat, user, N=3, simMeas=cosSim, estMethod=standEst): 54 unratedItems = nonzero(dataMat[user, :].A == 0)[1] # 寻找该用户未评分的物品 55 if len(unratedItems) == 0: return 'you rated everything' 56 itemScores = [] # 预测评分列表 57 for item in unratedItems: #枚举每一个未评分的物品,进行预测评分 58 estimatedScore = estMethod(dataMat, user, simMeas, item) 59 itemScores.append((item, estimatedScore)) 60 return sorted(itemScores, key=lambda jj: jj[1], reverse=True)[:N] # 对物品按预测评分进行降序排序
六.利用SVD进行数据压缩
1 def printMat(inMat, thresh=0.8): # 输出图案 2 for i in range(32): 3 for k in range(32): 4 if float(inMat[i, k]) > thresh: 5 print 1, 6 else: 7 print 0, 8 print '' 9 10 '''图片压缩, numSV为压缩后的维度''' 11 def imgCompress(numSV=3, thresh=0.8): 12 myl = [] 13 for line in open('0_5.txt').readlines(): # 读取图案 14 newRow = [] 15 for i in range(32): 16 newRow.append(int(line[i])) 17 myl.append(newRow) 18 myMat = mat(myl) 19 print "****original matrix******" 20 printMat(myMat, thresh) 21 U, Sigma, VT = la.svd(myMat) # 奇异值分解 22 SigRecon = mat(zeros((numSV, numSV))) 23 for k in range(numSV): # 选取前numSV个奇异值进行压缩 24 SigRecon[k, k] = Sigma[k] 25 reconMat = U[:, :numSV] * SigRecon * VT[:numSV, :] # 压缩后的图案 26 print "****reconstructed matrix using %d singular values******" % numSV 27 printMat(reconMat, thresh)