任务概述:将这张图片作为输入 , 然后抠出只有斑点的图片

灵感来源:
1. 黄色部分用绿色的掩盖掉得到图片B,然后A和B进行∩运算,相同的设置为0
2.统计单词的子母数,开辟一个26个元素的数组,进来一个字母在相应的地方++,类似hashmap
3.为什么要用Hue这个分量下手,因为这幅图就2个颜色,肯定会在2个地方突出来,然后中间的波谷
作为分隔点,其中一个突出来的部分置为0
4.Hue分量在[0,1]连续 变化 , 灰度值和R分量在【0,255】离散的变化,将【0,1】线性变化到【0,255】
R分量就像是随机变量X,自身只能离散的取值 , H分量是double类型的,取值是连续的
I=imread('375.png');
hv=rgb2hsv(I); %自带的函数就是good
H=hv(:,:,1);
S=hv(:,:,2);
V=hv(:,:,3); %也可以分别绘制H,S,V分量的图片
[M,N,D] = size(I);
vec = zeros(1,256) %初始化一个256元素的行矩阵
for i=1:M
for j=1:N
if( round( H(i,j)*255 ) == 0 )
array(1,1) = array(1,1) +0 ;
% if( round( H(i,j)*255 )==257 )
% array(1,256) = array(1,256) +1 ;
else
vec( 1 , round( H(i,j)*255 ) ) = vec( 1 , round( H(i,j)*255 ) ) + 1; %见备注图片 %改进自带的函数
end
end
end
%写入
Mat = array ;
fid = fopen('D:data.txt','wt');
[row,col] = size(Mat);
for i=1 : row
for j = 1:col
fprintf(fid,'%g
',Mat(i,j)); %换行
end
end
fclose(fid);
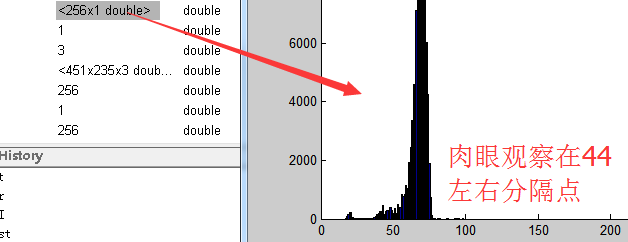
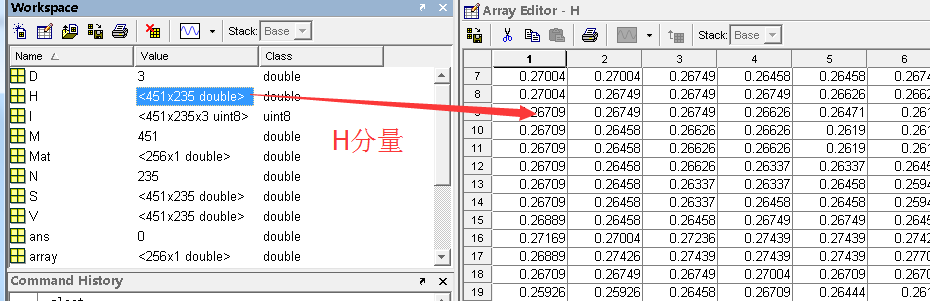
H_hist = imhist(H) 将451*235个值映射到[0,1]区间有多少(将H分量的所有取值映射到[0.255]这256个离散的点上:最精辟理解啊)
那个3段算法中也是将[0,x1]的任一一个点 映射到[0,y1] 这是一对一映射 ,上面那个是多对一映射

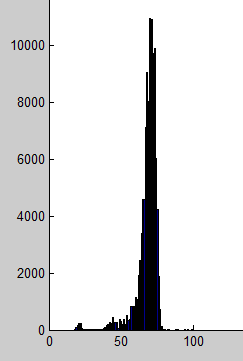
假设得到阈值(最后介绍方法) 44
这一步是将大于阈值的点统统处理掉
num = 44/255.0; %手动修改
[M,N] = size(H);
for i=1:M
for j=1:N
if( H(i,j) > num ) % 绿色部分显然要多些
V(i,j) = 0;
end; %V分量0是白色
end
end
V2 = V;
temp = cat(3,H,S,V2);
temp = hsv2rgb(temp);
imshow(temp);
实现--基于谷底最小值的阈值
1、描述:
此方法实用于具有明显双峰直方图的图像,其寻找双峰的谷底作为阈值,但是该方法不一定能获得阈值,对于那些具有平坦的直方图或单峰图像,该方法不合适。
2、实现过程:
该函数的实现是一个迭代的过程,每次处理前对直方图数据进行判断,看其是否已经是一个双峰的直方图,如果不是,则对直方图数据进行半径为1(窗口大小为3)的平滑,如果迭代了一定的数量比如1000次后仍未获得一个双峰的直方图,则函数执行失败,如成功获得,则最终阈值取两个双峰之间的谷底值作为阈值。
注意在编码过程中,平滑的处理需要当前像素之前的信息,因此需要对平滑前的数据进行一个备份。另外,首数据类型精度限制,不应用整形的直方图数据,必须转换为浮点类型数据来进行处理,否则得不到正确的结果。
知乎上还有人求这个判断双峰的算法
package erer;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.IOException;
import java.util.Arrays;
public class test {
public static int GetMinimumThreshold(int[] HistGram) {
int Y, Iter = 0;
double[] HistGramC = new double[256]; // 基于精度问题,一定要用浮点数来处理,否则得不到正确的结果
double[] HistGramCC = new double[256]; // 求均值的过程会破坏前面的数据,因此需要两份数据
for (Y = 0; Y < 256; Y++) {
HistGramC[Y] = HistGram[Y];
HistGramCC[Y] = HistGram[Y];
}
// 通过三点求均值来平滑直方图
while (IsDimodal(HistGramCC) == false) // 判断是否已经是双峰的图像了
{
HistGramCC[0] = (HistGramC[0] + HistGramC[0] + HistGramC[1]) / 3; // 第一点
for (Y = 1; Y < 255; Y++)
HistGramCC[Y] = (HistGramC[Y - 1] + HistGramC[Y] + HistGramC[Y + 1]) / 3; // 中间的点
HistGramCC[255] = (HistGramC[254] + HistGramC[255] + HistGramC[255]) / 3; // 最后一点
// // System.Buffer.BlockCopy(HistGramCC, 0, HistGramC, 0, 256 *
// sizeof(double));
System.arraycopy(HistGramCC, 0, HistGramC, 0, 256);
Iter++;
if (Iter >= 1000)
return -1; // 直方图无法平滑为双峰的,返回错误代码
}
// 阈值极为两峰之间的最小值
boolean Peakfound = false;
for (Y = 1; Y < 255; Y++) {
if (HistGramCC[Y - 1] < HistGramCC[Y] && HistGramCC[Y + 1] < HistGramCC[Y])
Peakfound = true;
if (Peakfound == true && HistGramCC[Y - 1] >= HistGramCC[Y] && HistGramCC[Y + 1] >= HistGramCC[Y])
return Y - 1;
}
return -1;
}
private static boolean IsDimodal(double[] HistGram) // 检测直方图是否为双峰的
{
// 对直方图的峰进行计数,只有峰数位2才为双峰
int Count = 0;
for (int Y = 1; Y < 255; Y++) {
if (HistGram[Y - 1] < HistGram[Y] && HistGram[Y + 1] < HistGram[Y]) {
Count++;
if (Count > 2)
return false;
}
}
if (Count == 2)
return true;
else
return false;
}
public static void main(String args[]) throws IOException {
File file = new File("D:\data.txt");// Text文件
BufferedReader br = new BufferedReader(new FileReader(file));// 构造一个BufferedReader类来读取文件
String s = null;
int[] data1 = new int[256];
int i = 0;
while ((s = br.readLine()) != null) {// 使用readLine方法,一次读一行
// System.out.println(s);
System.out.println("--------------");
try {
String str = s;
String str2 = str.replaceAll(" ", "");
System.out.println(str2);
data1[i] = Integer.parseInt(str2);
;
i++;
} catch (NumberFormatException e) {
e.printStackTrace();
}
System.out.println(Arrays.toString(data1));
System.out.println(data1.length);
}
br.close();
;
int[] HistGram = new int[256];
System.arraycopy(data1, 0, HistGram, 0, 256);
int num = GetMinimumThreshold(HistGram);
System.out.println("阈值是" + num);
}
}
得到阈值是28,运行
