相关博客：
（里面出现的内容，下面将不再重复）
主要内容：
一.单个样本向量化
二.多个样本向量化
三.激活函数及其导数
四.随机初始化
五.深层神经网络的前向与反向传播
六.参数和超参数
一.单个样本向量化
如下神经网络，对于第一层的神经元，每个神经元的输出，即a的计算如下：
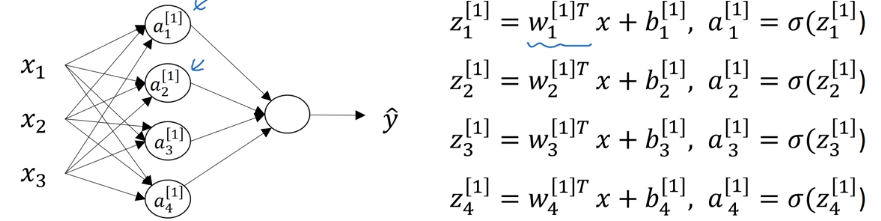
但是这种每个神经元的输出都单独计算的方式显得很繁琐，至少在写代码的时候就很容易出错。为了简化表示和提高效率，需要将其向量化，即把每一层的神经元看成是一个整体（一组向量）：
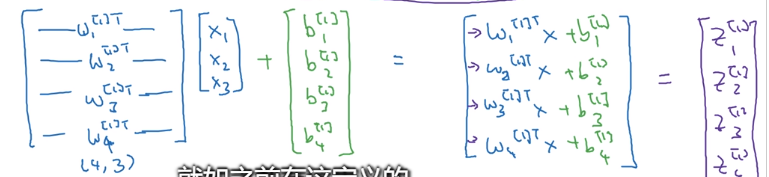
二.多个样本向量化
上面介绍了单个样本的向量化，如果有m个样本，那么可以使用一个for循环解决：
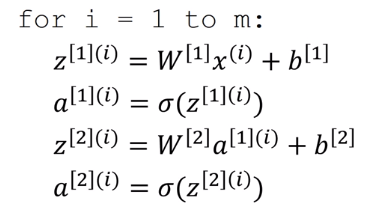（中括号里面的是第几层，小括号里面的是第几个样本）
但是，能不能把这m个样本在进一步向量化呢？能，规则就是把样本以列的形式叠在一起形成一个输入矩阵X（以往我们习惯了样本以行的形式堆叠，但在神经网络中以列堆叠更加方便）：
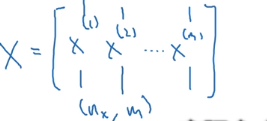
这样，就能去掉代码中的for循环了：
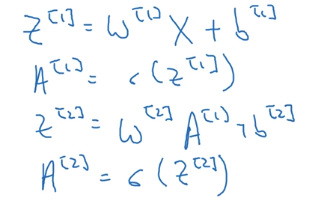
其中：
三.激活函数及其导数
1.sigmoid函数（没人用，因为|z|较大的时候，曲线的斜率非常小，梯度下降收敛变得非常慢。）
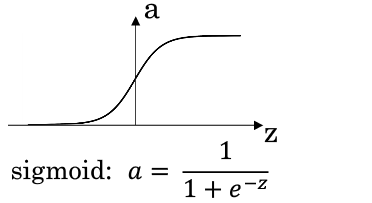
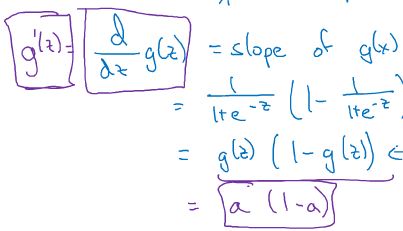
2.tanh函数（效果比sigmoid好，因为均值为0，带有去中心化的功能。但似乎还是没什么人用）：
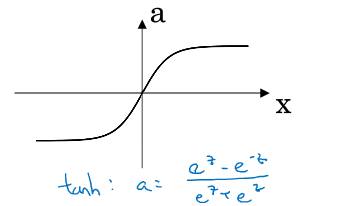
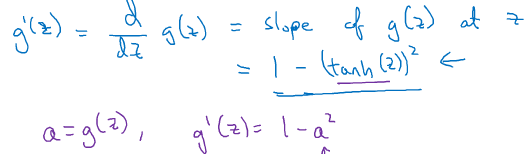
3.Relu函数（最多人用，但在z<0时不也斜率为0，梯度下降“降”不了吗？课程上说有方法可以使得z基本上大于0）：
4.leaky Relu函数：
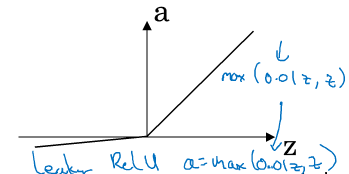
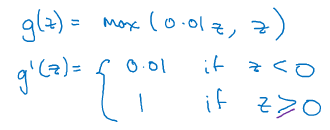
四.随机初始化
在以往的机器学习算法中，我们习惯把参数都初始化为0，但是这种做法不能应用于神经网络，因为这会使神经网络失效。为何失效？请看下文分解：
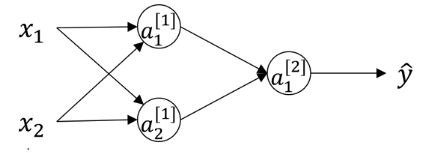
可知参数w代表着当前神经元或者说当前输入在下一层神经元所占的比重。对于第一层的两个神经元，如果我们把他们的参数w都设置为0，那么他们不管在前向传播还是在反向传播的过程中，干的事情、得到的结果都是一模一样的（根据对称性），所以神经网络就退化成一条“神经元链”了，一层中“多个神经元”就没有意义了。因此，需要随机初始化w，使得两个神经元“干的事情”不同。
五.深层神经网络的前向与反向传播
对于以下深层神经网络：
在前向传播的第l层，我们的工作是：输入a[l-1]，输出a[l]，同时将z[l]缓存起来，因为在反向传播的时候还要重新利用。如下：
在反向传播的第l层，我们的工作是：
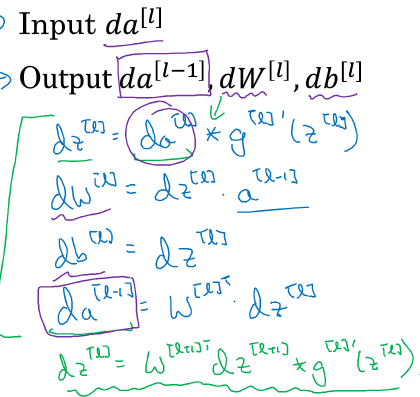
所以，BP神经网络的训练过程可以归结为以下流程：
六.参数和超参数
参数：如线性回归中的w和b，这类通过训练数据得出取值的参数就直接称为参数，特点是无需人为设定，算法已经解决了它们的取值。
超参数：如梯度下降的学习率α、正则项前面的参数C等等，这类无法通过算法去确定值，只能通过交叉检验取最优值或者直接根据人们经验而设定的参数，称为超参数。