16:33:56
2020-06-26
当然可以先看一下成绩:
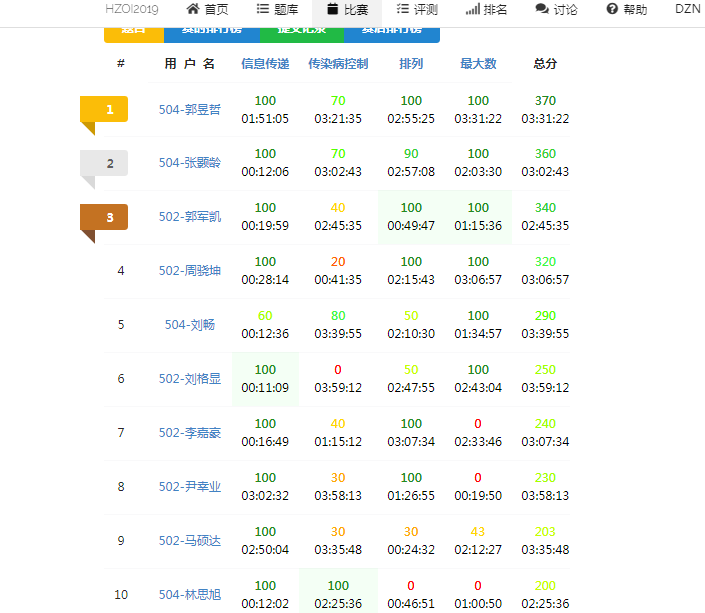

非常显然的成绩不能算有多好,当然其实这也可能是假期水课的报应 (额)
但是比我集训前想象的要好一点(集训时想象的是排名前30就可以,嗯?)
好了,毕竟是第一天,后面日子还长,相信结果不会烂的。
好了,现在看一下第一题:
第一题
原题来自洛谷P2661 :题目链接:https://www.luogu.com.cn/problem/P2661
比较显然的暴力思路(就是我写的)但是复杂度是O(n2)的,显然只有60分。
然后想正解,比较显然想到求一个最小环。但是如何求?
仔细观察这道题可以发现 每人只会把信息告诉一个人,也就是说只有一条出边
然后可以显然的发现图里只有简单环,那么我们可以想到求Tarjan强连通分量。
就是个裸板子,下面是代码:(注意只是这道题比较特殊,才能用Tarjan水过)
#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn=200005;
int a[maxn];
int Min=9999999;
int dfn[maxn],low[maxn],dfs_clock,sta[maxn],top,belong[maxn],siz[maxn],dcc;
void tarjan(int u){
dfn[u]=low[u]=++dfs_clock;
sta[++top]=u;
int v=a[u];
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(!belong[v])low[u]=min(low[u],dfn[v]);
if(dfn[u]==low[u]){
dcc++;
while(1){
int x=sta[top--];
belong[x]=dcc;
siz[dcc]++;
if(x==u)break;
}
if(siz[dcc]!=1) Min=min(siz[dcc],Min);
}
}
int main(){
//freopen("a.in","r",stdin);
int n;scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=n;i++){
if(!dfn[i])tarjan(i);
}
printf("%d",Min);
return 0;
}
但是就这样水过肯定是不行的,那么还有没有其他解法呢?
显然是有的。那就是带权并查集。
哎,假期没有认真听带权并查集,导致没有写出来,不过经过四分之一个时辰的努力。终于看懂了它。
然后我会在代码里加一些注释
代码:
#include <cstdio>
#include <algorithm>
using namespace std;
int fa[200005],d[200005];
int Min=0x3f3f3f3f;
int get(int x){
if(x==fa[x])return x;
else{
int last=fa[x];
fa[x]=get(fa[x]);
d[x]+=d[last];
return fa[x];
}
}
void merge(int x,int y){
int xx=get(x),yy=get(y);
if(xx!=yy){
fa[xx]=yy;
d[x]=d[y]+1;
}
else {
Min=min(Min,d[x]+d[y]+1);// d[x]+d[y]+1这个我会在后面加一张图解释。
}
}
int main(){
//freopen("a.in","r",stdin);
int n;scanf("%d",&n);
for(int i=1;i<=n;i++)fa[i]=i;//初始化
for(int i=1;i<=n;i++){
int x;scanf("%d",&x);
merge(i,x);
}
printf("%d",Min);
return 0;
}
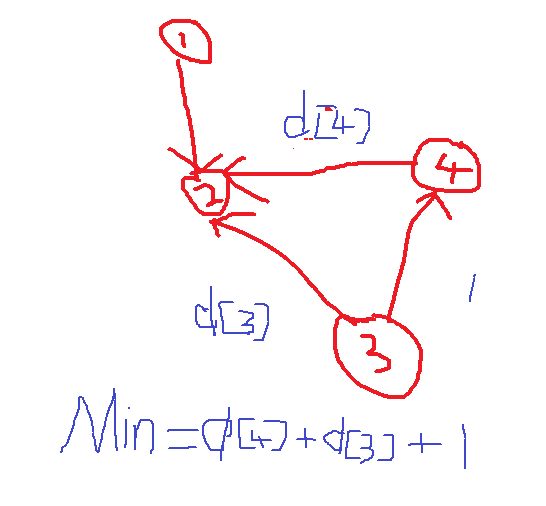
我觉得比较好理解(可能图比较烂)
第二题

这道题当时我是看错题意了,所以想成了树形DP,但成功水了三十分。
其实这道题没有正解,一般人都能想到贪心,但是贪心总是不能AC(80pts)
其实吧,不要想南么复杂,其实数据范围才300 ,直接爆搜(加一小小优化)就能过,
但是代码比较不大好写(本人目前还没有成功写出)
所以代码暂时不给了,先说一下思路:
首先dfs 一遍 求出 deep深度,size 子树大小,和father父亲。
然后依次每一深度枚举切断的边就行了。
代码到时会给的。。。。。。
OK 代码终于来了:
#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=605;
int n,m;
int Min=9999999;
int mdeep;
int dis[maxn][maxn],cnt1[maxn];
struct edge{
int to,next;
}e[maxn];int head[maxn],cnt=0;
void add(int x,int y){
e[++cnt].to=y;e[cnt].next=head[x];head[x]=cnt;
}
int size[maxn],fa[maxn],deep[maxn];
void dfs(int u,int f){
for(int i=head[u];i;i=e[i].next){
int v=e[i].to;
if(v==f)continue;
deep[v]=deep[u]+1;
fa[v]=u;
mdeep=max(mdeep,deep[v]);
dfs(v,u);
}
}
int cut[maxn];
void biaoji(int u,int ji){
cut[u]=ji;
for(int i=head[u];i;i=e[i].next){
int v=e[i].to;
if(v==fa[u])continue;
biaoji(v,ji);
}
}
int dfs3(int dep){
int sum=0;
for(int i=1;i<=cnt1[dep];i++){
if(cut[dis[dep][i]]==0)sum++;
}
return sum;
}
void dfs2(int dep,int sum){
if(sum>=Min)return;
if(dep>mdeep||dfs3(dep)==0){
//printf("%d ",sum);
Min=min(Min,sum);return;
}
for(int i=1;i<=cnt1[dep];i++){
int to=dis[dep][i];
if(cut[to]==1)continue;
biaoji(to,1);
//printf("%d ",dfs3(dep));
dfs2(dep+1,sum+dfs3(dep));
biaoji(to,0);
}
}
int main(){
//freopen("a.in","r",stdin);
int n,m;scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
int x,y;scanf("%d%d",&x,&y);
add(x,y);add(y,x);
}
dfs(1,0);
for(int i=1;i<=n;i++){
dis[deep[i]][++cnt1[deep[i]]]=i;
}
dfs2(1,1);
printf("%d",Min);
return 0;
}
第三题
题目来源:洛谷P4163 [SCOI2007] 链接:https://www.luogu.com.cn/problem/P4163

这道题其实我当时就没思路。
这道题解法很多:
有状压DP,有直接爆搜,当然我今天不想说这两种方法
我想说C++STL解法(简单)
首先介绍一个STL容器:
next_permutation
它可以从递增数列(一定要是递增的,不然不是全排列)求出全排列组合(就是求出的排列是从小到大)。
非常好用,但是有一个问题就是一定要会拼写(我就是没拼出来)
来一起拼三遍: next_permutation,next_permutation,next_permutation
下面就非常简单,模拟就完了。
代码:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int main(){
//freopen("a.in","r",stdin);
int t;scanf("%d",&t);
while(t--){
char s[15];int a[15];
int d;
scanf("%s%d",s,&d);
int len=strlen(s);
for(int i=0;i<len;i++){
a[i+1]=s[i]-'0';
}
sort(a+1,a+len+1);
int cnt=0;
while(1){
long long ans=0;
for(int i=1;i<=len;i++){
ans=ans*10+a[i];
}
if(ans%d==0)cnt++;
if(next_permutation(a+1,a+len+1)==0)break;
}
printf("%d
",cnt);
}
return 0;
}
应该非常显然。
第四题

第四题是我唯一AC的一道题,就是线段树。
当然树状数组和单调队列也能解决。
然后直接上代码了
#include <cstdio>
#include <algorithm>
#define ll long long
using namespace std;
const int maxn=200005;
ll tree[maxn<<2],a[maxn];
ll n,d;
ll t=0;
ll cnt=0;
void modify(int rt,int l,int r,ll x,ll y){
if(l==r){
tree[rt]=max(tree[rt],y);return;
}
int mid=(l+r)/2;
if(x<=mid)modify(rt<<1,l,mid,x,y);
else modify(rt<<1|1,mid+1,r,x,y);
tree[rt]=max(tree[rt<<1],tree[rt<<1|1]);
}
ll query(int rt,int l,int r,ll s,ll t){
if(s<=l&&r<=t){
return tree[rt];
}
int mid=(l+r)/2;
if(t<=mid)return query(rt<<1,l,mid,s,t);
else if(s>mid)return query(rt<<1|1,mid+1,r,s,t);
else return max(query(rt<<1,l,mid,s,t),query(rt<<1|1,mid+1,r,s,t));
}
int main(){
//freopen("a.in","r",stdin);
scanf("%lld%lld
",&n,&d);
for(int i=1;i<=n;i++){
char c;scanf(" %c ",&c);
if(c=='A'){
ll x;scanf("%lld",&x);
x=(x%d+t%d)%d;
modify(1,1,n,++cnt,x);
}
else {
ll l;scanf("%lld",&l);
if(cnt==0){
printf("0
");continue;
}
t=query(1,1,n,cnt-l+1,cnt);
printf("%lld
",t);
}
}
return 0;
}
OK,集训的第一次正式考试就结束了。
以此为戒,面向未来