[题目描述]
给定一个长度为 N 的正整数序列{ܽܰ},设数对(i,j)的得分 Sij=|ai-aj|,你需要找出 K 对数,使得这 K 对数的得分之和最小。
[输入格式]
第一行有两个正整数 N,K,如题所述。接下来一行有 N 个正整数,表示序列中的数。 [输出格式] 只有一个数,表示最小的得分之和。
[样例输入]
5 5 5 3 1 4 2
[样例输出]
6
[样例解释]
以下括号里的数表示下标。
选择(1,4),(2,4),(2,5),(3,5)这 4 对数,得分之和为 4。再从(1,2),(2,3),(4,5)中任选 1 对,因为这 3 对的得分都一样,都为 2。选择的数对(i,j)中 i,j 不能相等,且(i,j),(j,i)表示同一个数对,也就是说只能选其中一个。
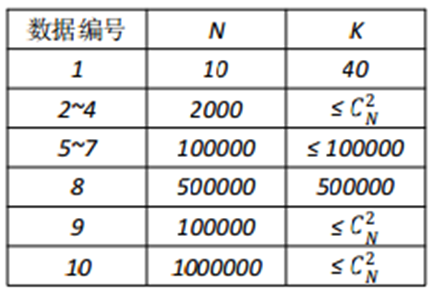
[数据范围]
对于 100%的数据:ai≤10 8,保证答案不超过 int64 范围。
题解:
①根据数据范围可以得出,最后的二元组(i,j)早已超过可以一一枚举统计答案的范围。
②当发现++式统计答案会T的时候,考虑数学公式、二分等。
③二分最大差值,判断时用单调队列维护最长小于等于二分差值的窗口,统计二元组个数。
④一个细节:假如二分到x超过了k个,x-1的时候不超过k个,那么意思说k没有满,那么直接剩余个数乘上x就可以了。
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
using namespace std;
ll a[1000006];
ll ans,k;
ll n;
void read(ll &x){
static ll f; static char ch;
x=0; f=1; ch=getchar();
while(ch<'0'||'9'<ch){if(ch=='-')f=-1;ch=getchar();}
while('0'<=ch&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
x=x*f;
}
ll check(ll lim){
ll j=1; ll cnt=0,sum=0; ans=0;
for(ll i=1;i<=n;i++){
while(j<i&&lim<a[i]-a[j]) sum-=a[j],j++;
cnt+=i-j; ans+=a[i]*(i-j)-sum;
sum+=a[i];
}
return cnt;
}
void binary(ll l,ll r){
ll mid,maxder=0;
while(l<=r){
mid=(l+r)>>1;
if(check(mid)>=k) maxder=mid,r=mid-1;
else l=mid+1;
}
ll kk=check(maxder-1);
ans+=maxder*(k-kk);
cout<<ans;
}
int main(){
freopen("mark.in","r",stdin);
freopen("mark.out","w",stdout);
read(n); read(k);
for(ll i=1;i<=n;i++) read(a[i]);
sort(a+1,a+n+1);
binary(0,a[n]-a[1]);
return 0;
}//*ZJ