题目描述
无向连通图 G 有 n 个点,n−1 条边。点从 1 到 n 依次编号,编号为 i 的点的权值为 Wi,每条边的长度均为 1。图上两点 (u,v) 的距离定义为 u 点到 v 点的最短距离。对于图 G 上的点对 (u,v),若它们的距离为 2,则它们之间会产生Wv×Wu 的联合权值。
请问图 G 上所有可产生联合权值的有序点对中,联合权值最大的是多少?所有联合权值之和是多少?
输入输出格式
输入格式:
第一行包含 1 个整数 n。
接下来 n−1 行,每行包含 2 个用空格隔开的正整数 u,v,表示编号为 u 和编号为 v 的点之间有边相连。
最后 1 行,包含 n 个正整数,每两个正整数之间用一个空格隔开,其中第 i 个整数表示图 G 上编号为 ii 的点的权值为 Wi。
输出格式:
输出共 1 行,包含 2 个整数,之间用一个空格隔开,依次为图 G 上联合权值的最大值和所有联合权值之和。由于所有联合权值之和可能很大,输出它时要对10007取余。
输入输出样例
说明
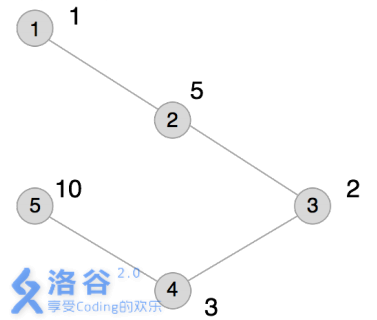
本例输入的图如上所示,距离为2 的有序点对有(1,3) 、(2,4) 、(3,1) 、(3,5)、(4,2) 、(5,3)。
其联合权值分别为2 、15、2 、20、15、20。其中最大的是20,总和为74。
【数据说明】
对于30%的数据,1<n≤100;
对于60%的数据,1<n≤2000;
对于100%的数据,1<n≤200000,0<Wi≤10000。
保证一定存在可产生联合权值的有序点对。
这题好难啊啊啊啊!相信我这是道好题!
解析:
先BB几句:
一开始暴力只得了70分。。。暴力思路我也说一下吧:
把联合权值分成两个部分,如果我们看到一个点,关于这个点的联合权值一种是爷爷×儿子,一种是儿子×儿子。
爷爷×儿子我拿个倍增做了,儿子×儿子我没办法了,想不出优化方法,只能爆搜一遍找两个儿子。复杂度大概是O(n^3),只得了70分。
就是这样:
#include<cstdio> #include<iostream> #include<cmath> #include<algorithm> #include<cstring> #include<queue> #define N 200010 #define mod 10007 using namespace std; queue<int> q; int n,head[N],tot,w[N],f[N][30],t,d[N]; struct rec{ int next,ver; }g[N<<1]; void add(int x,int y){ g[++tot].ver=y; g[tot].next=head[x],head[x]=tot; } void reset(int x) { memset(d,0,sizeof(d)); q.push(x); d[x]=1; while(q.size()) { int index=q.front();q.pop(); for(int i=head[index];i;i=g[i].next){ int y=g[i].ver; if(d[y]) continue; d[y]=d[x]+1; f[y][0]=index; for(int j=1;j<=t;j++) f[y][j]=f[f[y][j-1]][j-1]; q.push(y); } } } int main() { scanf("%d",&n); t=(int)(log(n)/log(2)+1); for(int i=1;i<n;i++){ int u,v; scanf("%d%d",&u,&v); add(u,v);add(v,u); } for(int i=1;i<=n;i++) scanf("%d",&w[i]); reset(1); int ans=0,cnt=0; for(int i=1;i<=n;i++){ int tmp=w[i]*w[f[i][1]]; ans=max(tmp,ans); cnt=(cnt%mod+tmp%mod)%mod; } cnt<<=1; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++){ if(i==j) continue; if(f[i][0]==f[j][0]){ int tmp=w[i]*w[j]; ans=max(ans,tmp); cnt=(cnt%mod+tmp%mod)%mod; } } printf("%d %d ",ans,cnt); return 0; }
要AC正解的话,这道题似乎有三种解法。一种树形dp,一种dfs,一种非dfs。
某dalao跟我说的思路估计是dfs,但是我想到了非dfs。不过由于too yuong too simple,看了题解才后知后觉,我一直搞不清楚怎么去算它们的联合权值和。
主要在于这个乘法分配律啊,题解dalao居然用如此巧妙的方式解决了求权值和的问题。还有另一种方法需要一点数学技巧。
说说我的思路:
遍历一遍所有点,将所有与这个点相邻的点分别求权值和,累加到答案,得到权值和;
找到与这个点相邻的两个较大权值的点,求他们的联合权值(就是乘起来),更新最大值。
完事。
首先求最大的联合权值很简单。但是关键就在于我上面讲的,怎么求联合权值和这个问题上。
我一开始冥思苦想,怎么就是想不出怎么求某个点的3个相邻点之间所有的联合权值和,试了很多方法都不行。
至于为什么说3个相邻点,仔细想想,这是棵树,一个点最多连3条边。
看题解说乘法分配律?woc,真的没想到居然可以这样(也可以理解成加法结合律)。
也就是说,我们每次先求出这三个相邻点其中两个节点的联合权值,累加到答案中,再把它们两个的权值加起来,跟第三个相邻点相乘!这就相当于每个节点之间都乘了一次。
比如说这三个相邻节点是x,y,z,我们先求出x*y,再求出(x+y)*z,就相当于求出了x*z+y*z,但是注意,由于是我们只求出了单向的一次,所以最终答案要*2。
这种思路的AC代码(也是我的代码):
#include<cstdio> #include<iostream> #include<cmath> #include<algorithm> #include<cstring> #include<queue> #define N 200010 #define mod 10007 using namespace std; int n,head[N],tot; long long w[N]; struct rec{ int next,ver; }g[N<<1]; void add(int x,int y){ g[++tot].ver=y; g[tot].next=head[x],head[x]=tot; } int main() { scanf("%d",&n); for(int i=1;i<n;i++){ int u,v; scanf("%d%d",&u,&v); add(u,v);add(v,u); } for(int i=1;i<=n;i++) scanf("%lld",&w[i]); long long ans=0; long long maxx=0,t,mnow; for(int i=1;i<=n;i++){ int now=head[i]; t=(mnow=w[g[now].ver])%mod; now=g[now].next; for(;now;now=g[now].next){ int y=g[now].ver; maxx=(maxx%mod+(t*w[y])%mod)%mod; ans=max(mnow*w[y],ans); mnow=max(mnow,w[y]); t=(t%mod+w[y]%mod)%mod; } } printf("%lld %lld ",ans,(maxx<<1)%mod); return 0; }
还有一种思路,容我借张图。
给出dalao题解:戳这里
思路:
1、联合的两个节点距离为二,所以必定有一个中转点。所以,我们可以枚举每一个中转点。
2、假设每个中转点周围有两个点,权值分别为a、b,则联合权值为2ab=(a+b)^2-(a^2+b^2)。
3、若有三个点,权值分别为a、b、c,则联合权值为2ab+2bc+2ac=(a+b+c)^2-(a^2+b^2+c^2)。
4、综上,以某个节点为中转点的联合权值之和等于权值和的平方减去权值的平方和。
5、为了找到最大的联合权值,只需找到周围最大的两个权值max1,max2,相乘判断即可。
假设与某个点相邻的点为vi,我们有联合权值和:

这就是这个点可以求出的联合权值。
代码就不贴了,我又没写(逃