20191212模拟赛 问题B

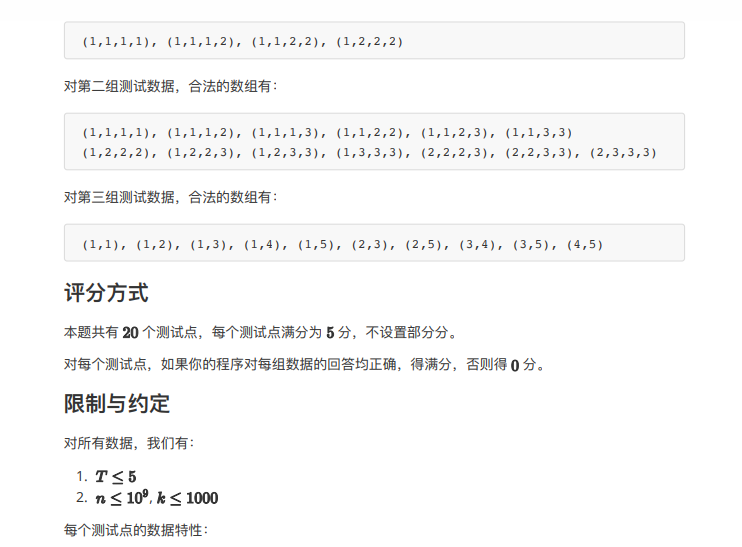
题目：

 

 

 

分析：

上来看到k=2,。。。

SB杜教筛phi

有点感冒，这把养生一点。。。

于是写了55分走人了。。

下来一看挺简单的啊2333

不考虑gcd时，构造数列的方案为C(N+K-1,K)

考虑gcd时，就要套mu了

ans=sigma(i=1...n)mu[i]*F(n/i)

其中f(x)=C(x+K-1,K)

然后有一个公式。。。

summu[n]=1-sigma(d=2...n)summu[n/d]

这样就可以n^(2/3)求summu了

对于F，由于K很小，可以暴力算。。。

但是这样极限数据会很卡诶。。。

考虑F分段处理

当x+K-1小于1e6时，可以预处理组合数

又由于x+K-1大于1e6的情况很少。。。

所以是可以过的2333。。。。

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
#include<map>

#define maxn 1000005
#define INF 0x3f3f3f3f
#define MOD 1000000007

using namespace std;

inline int getint()
{
    int num=0,flag=1;char c;
    while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;
    while(c>='0'&&c<='9')num=num*10+c-48,c=getchar();
    return num*flag;
}

int n,K;
int N=1000000;
int pri[maxn],cnt,np[maxn];
int mu[maxn];
long long fac[maxn],inv[maxn];
long long ans;
map<int,long long>M;

inline void init()
{
    mu[1]=1;
    for(int i=2;i<=N;i++)
    {
        if(!np[i])pri[++cnt]=i,mu[i]=-1;
        for(int j=1;j<=cnt&&i*pri[j]<=N;j++)
        {
            np[i*pri[j]]=1;
            if(i%pri[j]==0)break;
            mu[i*pri[j]]=-mu[i];
        }
    }
    for(int i=1;i<=N;i++)mu[i]+=mu[i-1];
    for(int i=1;i<=N;i++)(mu[i]+=MOD)%=MOD;
    fac[0]=fac[1]=inv[0]=inv[1]=1;
    for(int i=2;i<=N;i++)fac[i]=fac[i-1]*i%MOD;
    for(int i=2;i<=N;i++)inv[i]=inv[MOD%i]*(MOD-MOD/i)%MOD;
    for(int i=2;i<=N;i++)inv[i]=inv[i]*inv[i-1]%MOD;
}

inline long long solve(int x)
{
    if(x<=N)return mu[x];
    if(M.count(x))return M[x];
    long long num=1;
    for(int i=2,j;i<=x;i=j+1)
    {
        j=x/(x/i);
        (num-=(j-i+1)*solve(x/i)%MOD)%=MOD;
    }
    return M[x]=(num+MOD)%MOD;
}

inline long long C(int p,int q)
{return fac[p]*inv[q]%MOD*inv[p-q]%MOD;}

inline long long cal(int x)
{
    if(x+K-1<=N)return C(x+K-1,K);
    long long tmp=1;
    for(int i=1;i<=K;i++)tmp=tmp*((x+K-1)-i+1)%MOD;
    return tmp*inv[K]%MOD;
}

int main()
{
    int T=getint();
    init();
    while(T--)
    {
        M.clear();
        n=getint(),K=getint();
        ans=0;
        for(int i=1,j;i<=n;i=j+1)
        {
            j=n/(n/i);
            (ans+=(solve(j)-solve(i-1)+MOD)*cal(n/i)%MOD)%=MOD;
        }
        printf("%lld
",ans);
    }
}