联考20200725 T1 String

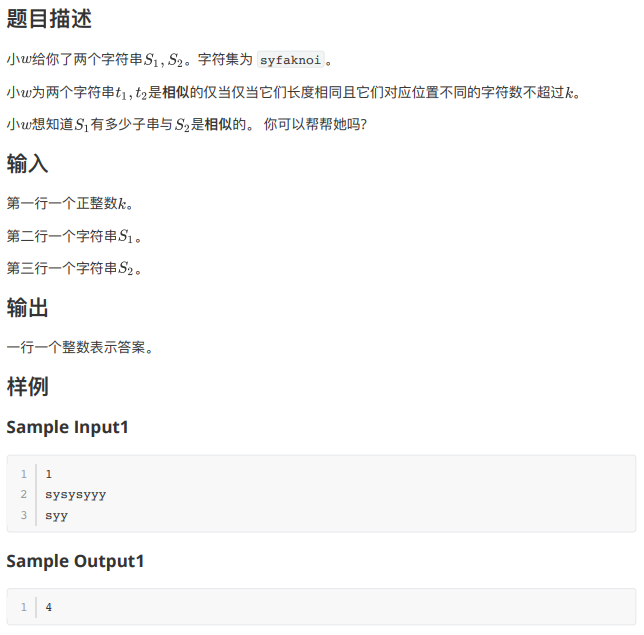
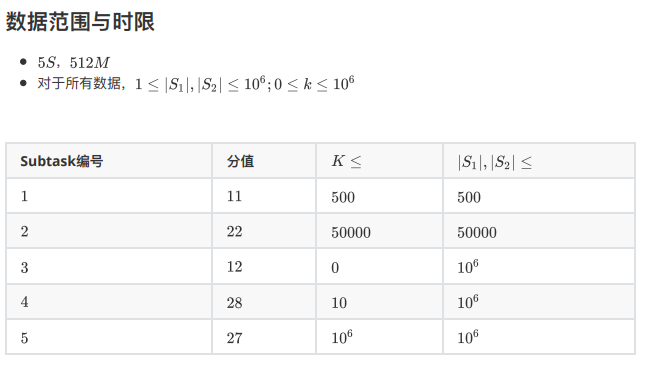
分析：
发现字符集大小只有8，时间限制是9s
对于每种字符(c)构建生成函数(f(x)=sum_{i=0}[S_i==c]x^i)
把(S_2)的生成函数翻转与(S_1)做卷积，得到的([|S_2|-1,|S_1|-1])的位置的值就是(S_1)中下标从([0,|S1|-|S2|])开始的字符相同数量
数据规模(10^6)，需要比较优秀的NTT实现
复杂度(O(8nlogn))

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>
#include<iostream>
#include<map>
#include<string>

#define maxn 3000005
#define MOD 998244353
#define Poly vector<int>

using namespace std;

inline int getint()
{
	int num=0,flag=1;char c;
	while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;
	while(c>='0'&&c<='9')num=num*10+c-48,c=getchar();
	return num*flag;
}

int n,m,K;
char S1[maxn],S2[maxn];
int Id[128];
int A[8][maxn],B[8][maxn];
int ans[maxn];
int Wl,Wl2,w[maxn<<2];
int rev[maxn<<2];

inline int upd(int x){return x<MOD?x:x-MOD;}
inline int ksm(int num,int k)
{
	int ret=1;
	for(;k;k>>=1,num=1ll*num*num%MOD)if(k&1)ret=1ll*ret*num%MOD;
	return ret;
}

inline void init(int N)
{
	Wl=w[0]=1;
	while((Wl<<1)<=N)Wl<<=1;
	w[1]=ksm(3,(MOD-1)/(Wl<<1)),Wl2=Wl<<1;
	for(int i=2;i<=Wl2;i++)w[i]=1ll*w[i-1]*w[1]%MOD;
}

inline void NTT(int *a,int opt,int N)
{
	for(int i=0;i<N;i++)if(i<rev[i])swap(a[i],a[rev[i]]);
	for(int i=1,B=Wl;i<N;i<<=1,B>>=1)
		for(int j=0,t=i<<1;j<N;j+=t)for(int k=0,x=0;k<i;k++,x+=B)
		{
			int v=1ll*a[i+j+k]*w[opt==1?x:Wl2-x]%MOD;
			a[i+j+k]=upd(a[j+k]-v+MOD),a[j+k]=upd(a[j+k]+v);
		}
	if(!~opt)for(int i=0,Inv=ksm(N,MOD-2);i<N;i++)a[i]=1ll*a[i]*Inv%MOD;
}

int main()
{
	K=getint();
	scanf("%s%s",S1,S2);
	Id['s']=0,Id['y']=1,Id['f']=2,Id['a']=3,Id['k']=4,Id['n']=5,Id['o']=6,Id['i']=7;
	n=strlen(S1),m=strlen(S2);reverse(S2,S2+m);
	K=m-K;
	for(int i=0;i<n;i++)A[Id[S1[i]]][i]=1;
	for(int i=0;i<m;i++)B[Id[S2[i]]][i]=1;
	int len=1;
	while(len<n+m)len<<=1;
	for(int i=0;i<len;i++)rev[i]=(rev[i>>1]>>1)|(i&1?len>>1:0);
	init(n+m);
	for(int k=0;k<8;k++)
	{
		NTT(A[k],1,len),NTT(B[k],1,len);
		for(int i=0;i<len;i++)A[k][i]=1ll*A[k][i]*B[k][i]%MOD;
		NTT(A[k],-1,len);
		for(int i=m-1;i<n;i++)ans[i]+=A[k][i];
	}
	int num=0;
	for(int i=m-1;i<n;i++)num+=(ans[i]>=K);
	printf("%d
",num);
}