【模板】线段树-单点修改，区间查询

容易理解但是难打（又长又难调）------仅代表个人观点

（能别打就别打）

线段树是什么？

大概长这样？（表示区间1到6）

线段树是一颗二叉树，是通过二分思想建立的一颗表示区间关系的树形结构。（总之记住它很好用就对了）

怎样建一颗线段树

大概思路：

二分+递归

没什么好讲的，具体看代码吧。。

//建树
struct node
{
  int a,b;
}tree[100001];

void make_tree(int p,int x,int y)//p为当前节点编号，x,y为区间的左右端点 
{
    tree[p].a=x;
    tree[p].b=y;
    if(x<y)
    {
        int mid=(x+y)/2;
        make_tree(p*2,x,mid);//左子树 
        make_tree(p*2+1,mid+1,y);//右子树 
    } 
}

表示区间[1,n]的线段树有多少个节点？

（不要看它看起来没什么用的样子，还是很重要的）

还是开到4*n吧，保险。

线段树怎么用？

单点修改

大概思路：

二分+递归找点，修改

代码：

//单点修改 
void adds(int p,int x,int V)
{
    tree[p].v+=V;//在每一个含有x的区间的权值上加上V 
    if(tree[p].a==tree[p].b)
    return;
    if(x<=tree[p*2].b)
    adds(p*2,x,V);//如果x在当前区间的左儿子里 
    if(x>=tree[p*2+1].a)
    adds(p*2+1,x,V); //如果在右儿子里 
}

（看不懂的话下面有图）（这图不是我画的）

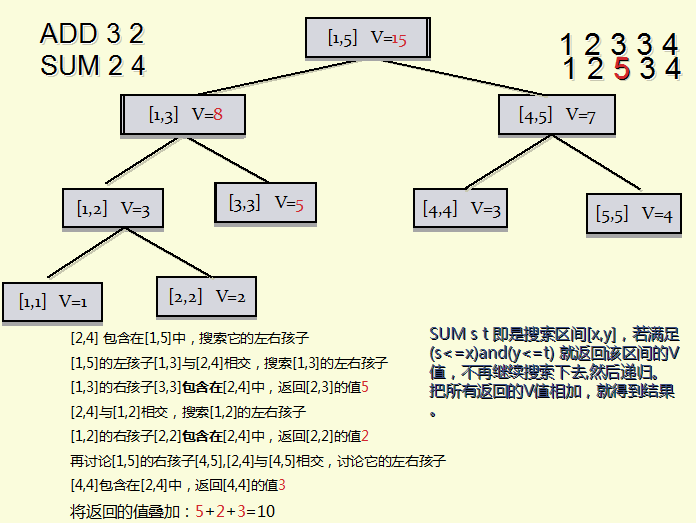
区间查询

大概思路：

二分+递归，如果在[x,y]里就加上当前区间的权值，如果不在就不加。

代码：

//区间查询
int ans;
void find(int x,int y,int p)
{
    if(tree[p].a>=x&&tree[p].b<=y)//如果当前区间正好在[x,y]里面 
    {
        ans+=tree[p].v;
        return;
    }
    if(x<=tree[p*2].b)
    find(x,y,p*2);
    if(y>=tree[p*2+1].a)
    find(x,y,p*2+1);
    
} 

（上面的图有解说）

先来看道题：线段树区间修改+单点查询

冥想ing。。

AC代码：

#include<iostream>
#include<cstdio>
using namespace std;
//建树
struct node
{
  int a,b,v;
}tree[2000010];
int a[500010];
void make_tree(int p,int x,int y)//p为当前节点编号，x,y为区间的左右端点 ,v是权值 
{
    tree[p].a=x;
    tree[p].b=y;
    if(x<y)
    {
        int mid=(x+y)/2;
        make_tree(p*2,x,mid);//左子树 
        make_tree(p*2+1,mid+1,y);//右子树 
    } 
}
int input(int p)//储值 
{
    if(tree[p].a==tree[p].b)
    {
        tree[p].v=a[tree[p].a];
        return tree[p].v;
    }
    tree[p].v=input(p*2)+input(p*2+1);
    return tree[p].v;
}
//单点修改 
void adds(int p,int x,int V)
{
    tree[p].v+=V;//在每一个含有x的区间的权值上加上V 
    if(tree[p].a==tree[p].b)
    return;
    if(x<=tree[p*2].b)
    adds(p*2,x,V);//如果x在当前区间的左儿子里 
    if(x>=tree[p*2+1].a)
    adds(p*2+1,x,V); //如果在右儿子里 
}
//区间查询
int ans;
void find(int x,int y,int p)
{
    if(tree[p].a>=x&&tree[p].b<=y)//如果当前区间正好在[x,y]里面 
    {
        ans+=tree[p].v;
        return;
    }
    if(x<=tree[p*2].b)
    find(x,y,p*2);
    if(y>=tree[p*2+1].a)
    find(x,y,p*2+1);
    
} 
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    scanf("%d",&a[i]);
    make_tree(1,1,n);
    input(1);
    int A,B,C;
    for(int i=1;i<=m;i++)
    {
        scanf("%d",&A);
        if(A==1)
        {
            scanf("%d%d",&B,&C);
            adds(1,B,C); 
        }
        else
        {
            ans=0;
            scanf("%d%d",&B,&C);
            find(B,C,1);
            printf("%d
",ans);
        }
    }
    return 0;
}