CF1428 F.Fruit Sequences

题目链接：传送门

题目思路：

以i 为右端点 ，令 h[j] = s[j]=='0'? 0 : h[j+1]+1 ,其中 j < i ;

枚举右端点i ， 对于任意一个左端点j ，其f(j,i) = max ( h[j] , h[j+1] , ... , h[i] ); 显然,对于固定的右端点 i ,向前枚举左端点j ， 其f值是单调不减的 , f(j,i) <= f(j-1,i) <= ... <= f(1,i) 。

那么用一个线段树维护一下f(j,i) 的和 即可【 [j,j]的值 = f(j,i），那么[1,i] = Σⁱ_j=1 f(j,i) ，用线段树维护区间和】。具体细节如下：

1. 如果 s[i] == '0' ， 由于 0 不会影响 h[j] 的值 ，所以直接求 [1,i] 的和即可

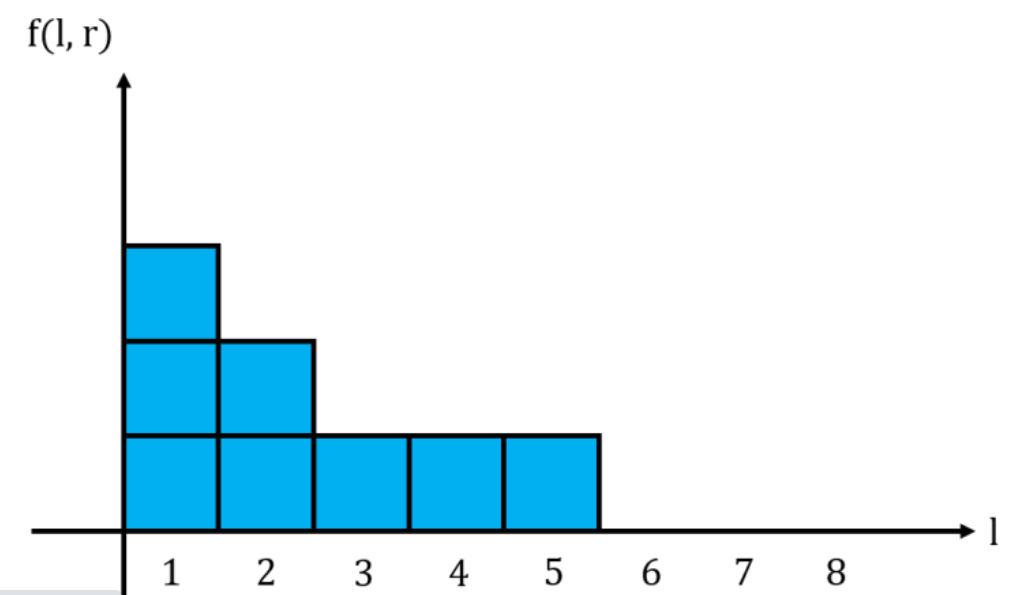
2. 如果 s[i] == '1' ， 由于 1 会影响i之前（包括i）这一段连续的‘1’ 的 h[j]值 ， 因此需要更新 [ last , i ] 区间 所有元素+1 ，其中last 为这段连续1 的起点；再更新 [x,last-1] 区间所有元素赋值为 h[last] ， x为满足h[x]  < h[last] && f(x,i) <= h[last] 的最小位置；（显然如果有比h[last] 大的 h[x] 值 , 那么 j <x , f(j,i) > h[last] 的，而小于h[last]的对应的x ， x<=j<=last , f(j,last) = h[last] ）;

（图片截止 原codeforces 题解）

代码：

#include<bits/stdc++.h>
/*
#include<cstdio>
#include<cmath>
#include<cstring>
#include<vector>
#include<cctype>
#include<queue>
#include<algorithm>
#include<map>
#include<set>
*/
#pragma GCC optimize(2)
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int,int> pii;
typedef pair<LL,LL> pLL;
typedef pair<double,double> pdd;
const int N=5e5+5;
const int M=8e5+5;
const int inf=0x3f3f3f3f;
const LL mod=1e8+7;
const double eps=1e-5;
const long double pi=acos(-1.0L);
#define ls (i<<1)
#define rs (i<<1|1)
#define fi first
#define se second
#define pb push_back
#define eb emplace_back
#define mk make_pair
#define mem(a,b) memset(a,b,sizeof(a))
LL read()
{
    LL x=0,t=1;
    char ch;
    while(!isdigit(ch=getchar())) if(ch=='-') t=-1;
    while(isdigit(ch)){ x=10*x+ch-'0'; ch=getchar(); }
    return x*t;
}
LL c[N<<2],ma[N<<2],lz[N<<2],fz[N<<2];
inline void pushdown(int i,int l,int r)
{
    if(fz[i])
    {
        LL &x=fz[i];
        int mid=l+r>>1;
        c[ls]=1LL*x*(mid-l+1);
        c[rs]=1LL*x*(r-mid);
        ma[ls]=ma[rs]=x;
        fz[ls]=fz[rs]=x;
        x=lz[ls]=lz[rs]=0;
    }
    if(lz[i])
    {
        LL &x=lz[i];
        int mid=l+r>>1;
        c[ls]+=1LL*x*(mid-l+1);
        c[rs]+=1LL*x*(r-mid);
        ma[ls]+=x; ma[rs]+=x;
        lz[ls]+=x; lz[rs]+=x;
        x=0;
    }
}
void update(int i,int l,int r,int ll,int rr,int x,const int flag)
{
    if(ll<=l&&r<=rr)
    {
        if(flag) c[i]+=1LL*x*(r-l+1),ma[i]+=x,lz[i]+=x;
        else c[i]=1LL*x*(r-l+1),ma[i]=x,fz[i]=x,lz[i]=0;
        return ;
    }
    pushdown(i,l,r);
    int mid=l+r>>1;
    if(mid>=ll) update(ls,l,mid,ll,rr,x,flag);
    if(mid<rr) update(rs,mid+1,r,ll,rr,x,flag);
    c[i]=c[ls]+c[rs];
    ma[i]=max(ma[ls],ma[rs]);
}
int query(int i,int l,int r,int x)
{
    if(l==r) return l;
    pushdown(i,l,r);
    int mid=l+r>>1;
    if(x<=ma[rs]) return query(rs,mid+1,r,x);
    else return query(ls,l,mid,x);
}
char s[N];
int main()
{
    int n=read();
    scanf("%s",s+1);
    LL ans=0;
    int last=0;
    for(int i=1;i<=n;i++)
    {
        if(s[i]=='1')
        {
            if(!last) last=i;
            int x=query(1,1,n,i-last+1);
            //由于 [i+1,n] 这段区间的所有元素的值是为0的，所以可以直接线段树查询（先查右半区间，再查左半区间） 最远的x( x满足 h[x]<h[last] && f(x,i)<=h[last] )
            //当然也可以通过单调栈预处理出来每一个i 对应的 x；或者也可以通过二分线段树在线处理，但这道题可以直接查询 就没有必要套二分了；
            update(1,1,n,last,i,1,1);
            // 先查询后更新，避免查到h[last] = i-last+1
            if(x<last) update(1,1,n,x,last-1,i-last+1,0);
        }
        else last=0;
        ans+=c[1];
    }
    printf("%lld
",ans);
    return 0;
}