
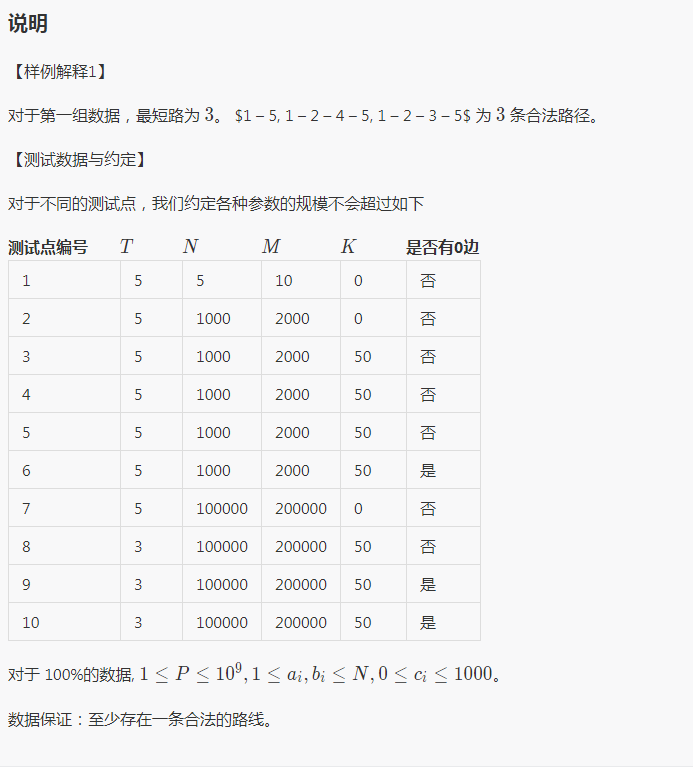
【题解】
先建反向图,用dijkstra跑出每个点到n的最短距离dis[i]
设f[u][k]表示dis(u,n)<=mindis(u,n)+k的方案数。对于边e(u,v,w),走了这条边的话需要多走的距离就是这条边的边权-原来u,v之间的距离,即w-(dis[u]-dis[v])
那么转移就是f[u][k]=sigma( f[v][k-w+(dis[u]-dis[v])] ),记忆化搜索非常好写。
判无数解的话记录当前状态是否在栈中就可以了。
1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #define LL long long 5 #define rg register 6 #define N 200010 7 using namespace std; 8 int T,n,m,k,p,tot,last[N],dis[N],pos[N],f[N][60]; 9 bool in[N][60]; 10 struct edge{int to,pre,dis;}e[N]; 11 struct heap{int p,d;}h[N]; 12 struct rec{int u,v,w;}r[N]; 13 inline int read(){ 14 int k=0,f=1; char c=getchar(); 15 while(c<'0'||c>'9')c=='-'&&(f=-1),c=getchar(); 16 while('0'<=c&&c<='9')k=k*10+c-'0',c=getchar(); 17 return k*f; 18 } 19 inline void MOD(int &k){if(k>=p) k-=p;} 20 inline void up(int x){ 21 int fa; 22 while((fa=x>>1)&&h[fa].d>h[x].d) swap(h[x],h[fa]),swap(pos[h[x].p],pos[h[fa].p]),x=fa; 23 } 24 inline void down(int x){ 25 int son; 26 while((son=x<<1)<=tot){ 27 if(h[son+1].d<h[son].d&&son<tot) son++; 28 if(h[son].d<h[x].d) swap(h[x],h[son]),swap(pos[h[x].p],pos[h[son].p]),x=son; 29 else return; 30 } 31 } 32 inline void dijkstra(int x){ 33 for(rg int i=1;i<=n;i++) dis[i]=1e9; 34 h[pos[x]=tot=1]=(heap){x,dis[x]=0}; 35 while(tot){ 36 int now=h[1].p; pos[h[tot].p]=1; h[1]=h[tot--]; if(tot) down(1); 37 for(rg int i=last[now],to;i;i=e[i].pre)if(dis[to=e[i].to]>dis[now]+e[i].dis){ 38 dis[to]=dis[now]+e[i].dis; 39 if(!pos[to]) h[pos[to]=++tot]=(heap){to,dis[to]}; 40 else h[pos[to]].d=dis[to]; 41 up(pos[to]); 42 } 43 } 44 } 45 int dfs(int x,int d){ 46 if(in[x][d]) return -1; 47 if(f[x][d]) return f[x][d]; 48 in[x][d]=1; f[x][d]=(x==n)?1:0; 49 for(rg int i=last[x],to,num;i;i=e[i].pre){ 50 int tmp=-dis[x]+dis[to=e[i].to]+e[i].dis; 51 if(tmp<=d){ 52 if((num=dfs(to,d-tmp))==-1) return -1; 53 MOD(f[x][d]+=num); 54 } 55 } 56 return in[x][d]=0,f[x][d]; 57 } 58 inline void Pre(){ 59 memset(in,0,sizeof(in)); 60 memset(last,0,sizeof(last)); 61 memset(pos,0,sizeof(pos)); 62 memset(f,0,sizeof(f)); 63 tot=0; 64 } 65 int main(){ 66 T=read(); 67 while(T--){ 68 Pre(); 69 n=read(); m=read(); k=read(); p=read(); 70 for(rg int i=1,u,v;i<=m;i++){ 71 r[i].u=u=read(); r[i].v=v=read(); 72 e[++tot]=(edge){u,last[v],r[i].w=read()}; last[v]=tot; 73 } 74 dijkstra(n); 75 memset(last,0,sizeof(last)); tot=0; 76 for(rg int i=1;i<=m;i++){ 77 int u=r[i].u,v=r[i].v; 78 e[++tot]=(edge){v,last[u],r[i].w}; last[u]=tot; 79 } 80 printf("%d ",dfs(1,k)); 81 } 82 return 0; 83 }