经典排序三剑客: 归并,堆排,快排。
今天,图解归并,一步步带你手撕代码~
归并排序,是采用"分而治之"思想的一个典型应用。
分治法精髓:
1.分 --- 将问题分解成若干个规模更小的问题
2.治 --- 将这些规模更小的问题逐个击破
3.合 --- 将已解决的子问题合并,最终得到"母"问题的解
知道了归并思想,如图,归并排序流程我们也能想到:
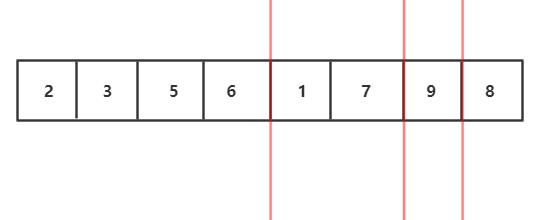
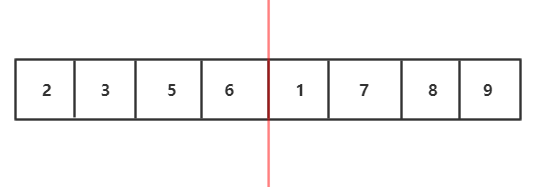
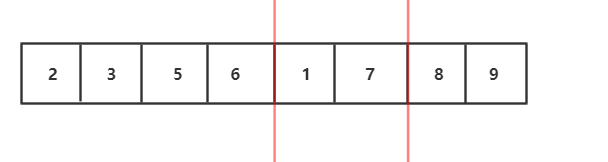
1.将待排序数组分解两个子序列,先让让左右两个子序列有序,然后再用两个有序数组合并的算法合并。那么怎么让左右子序列有序呢?
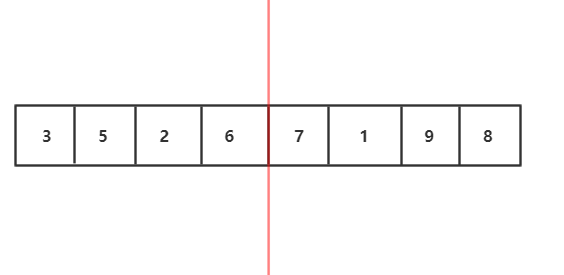
2.我们发现左右子序列还可以继续分解,左右子序列也可以通过自身的左右子序列排序后归并得到
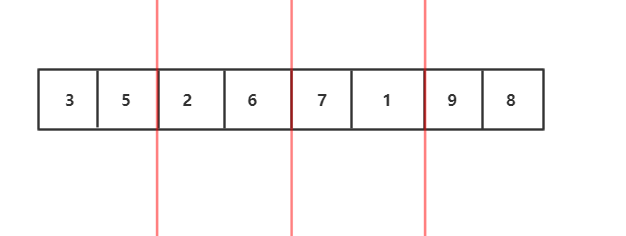
3.继续分解,分解到最小规模,也就是每个部分只有一个元素,我们发现每部分已经有序了
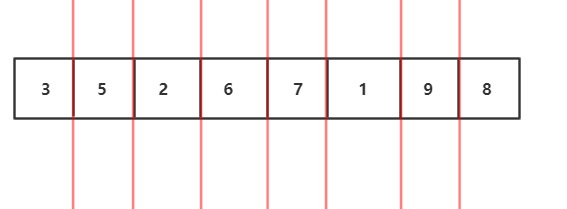
4.分治完,如图,开始用两个有序数组合并的算法合并,我们会发现这是一个递归过程,子问题的合并解就是该子问题"母问题"的解


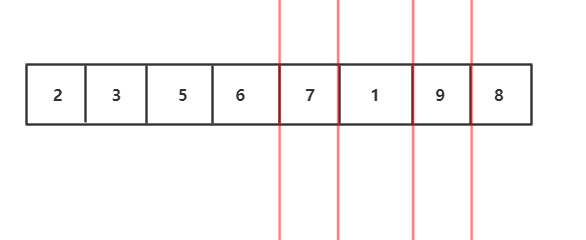

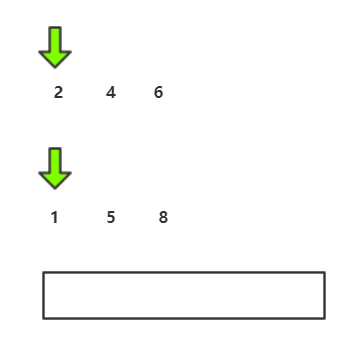
归并流程我们可以用递归实现,接下来要图解合并两个有序数组的算法 :
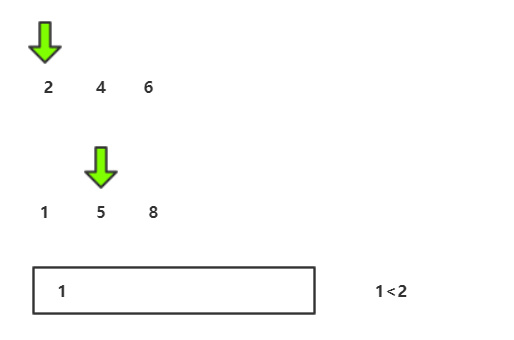
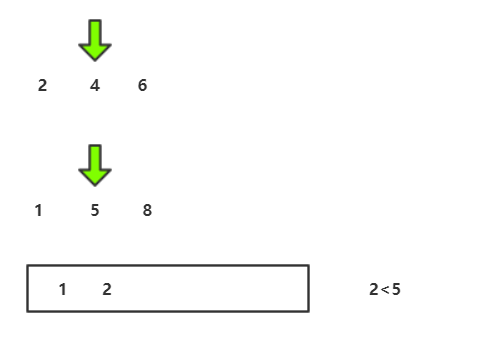
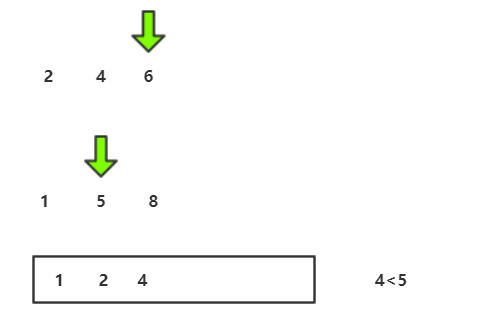
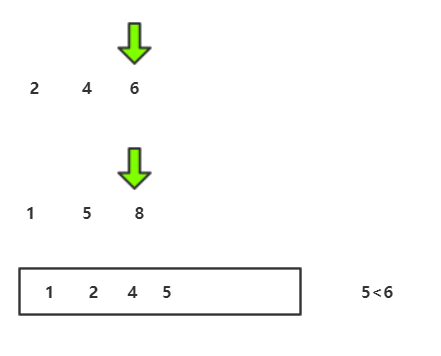
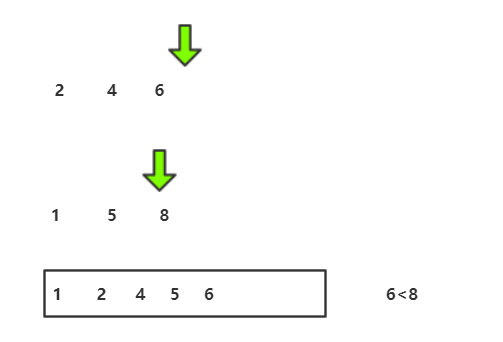
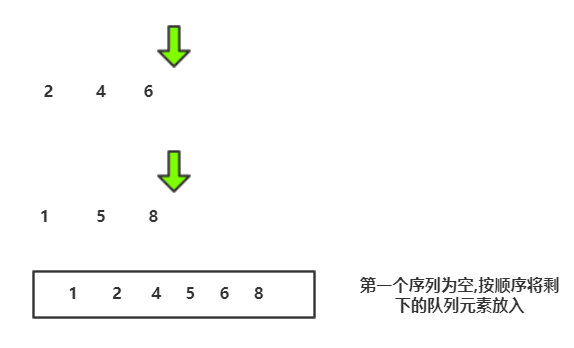
C代码实现:
#include<stdlib.h> #include<stdio.h> //归并两个有序数组 void Merge(int* a, int left, int mid, int right,int* tmp) { int begin1 = left, end1 = mid; int begin2 = mid+1, end2 = right; int index = left; //比较排序(双指针) while (begin1<=end1 && begin2<=right) { if (a[begin1] <= a[begin2]) { tmp[index++] = a[begin1++]; } else { tmp[index++] = a[begin2++]; } } //若剩余数组,按序插入 while (begin1 <= end1) tmp[index++] = a[begin1++]; while (begin2 <= end2) tmp[index++] = a[begin2++]; //拷贝到原数组 index = left; while (left <= right) { a[left++] = tmp[index++]; } } //分解成最小子问题,回溯归并 void Sort(int *a, int left, int right,int* tmp) { //递归终止条件 : 只剩一个元素 if (left >= right) return; int mid = left + (right-left)/2; Sort(a, left, mid,tmp); Sort(a, mid+1, right,tmp); Merge(a, left, mid, right,tmp); } //归并排序 void MergeSort(int *a, int n) { int* tmp = (int *)malloc(sizeof(int)*n); Sort(a, 0, n - 1, tmp); free(tmp); }
时间复杂度:O(nlogn)
空间复杂度:O(N),归并排序需要一个与原数组相同长度的数组做辅助来排序
稳定性: 稳定, 不管顺序如何,都要分解成最小子问题进行归并。