Contest Info
[Practice Link](https://codeforces.com/contest/1200)
| Solved | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| 5/6 | O | O | O | Ø | O | - |
- O 在比赛中通过
- Ø 赛后通过
- ! 尝试了但是失败了
- - 没有尝试
Solutions
A. Hotelier
代码:
#include <bits/stdc++.h>
using namespace std;
#define debug(...) { printf("# "); printf(__VA_ARGS__); puts(""); }
#define ll long long
const int N = 1e5 + 10;
int n, a[N];
char s[N];
void run() {
memset(a, 0, sizeof a);
cin >> (s + 1);
for (int i = 1; i <= n; ++i) {
if (s[i] == 'L') {
for (int j = 0; j <= 9; ++j) {
if (a[j] == 0) {
a[j] = 1;
break;
}
}
} else if (s[i] == 'R') {
for (int j = 9; j >= 0; --j) {
if (a[j] == 0) {
a[j] = 1;
break;
}
}
} else {
a[s[i] - '0'] = 0;
}
}
for (int i = 0; i <= 9; ++i)
cout << a[i];
cout << "
";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
while (cin >> n) run();
return 0;
}
B.Block Adventure
题意:
有(n)个房子,每个房子由(h_i)块积木搭成,能从第(i)个房子跳到第(i + 1)个房子当且仅当(|h_i - h_{i + 1}| leq k)。
但是你包里初始的时候有(m)块积木,你可以选择从包里拿出一些积木搭在你现在在的房子上,也可以将现在的房子的积木抽掉一些。
问能否从第(1)个房子都到第(n)个房子
思路:
如果当前房子的积木可以抽就尽量抽。
但是要注意抽取的时候要将当前高度和(k)取(Min)
代码:
#include <bits/stdc++.h>
using namespace std;
#define debug(...) { printf("# "); printf(__VA_ARGS__); puts(""); }
#define ll long long
const int N = 1e5 + 10;
int n, m, k, h[N];
void run() {
cin >> n >> m >> k;
for (int i = 1; i <= n; ++i) cin >> h[i];
for (int i = 1; i < n; ++i) {
if (h[i] < h[i + 1]) {
if (h[i + 1] - h[i] > k) {
if (m < (h[i + 1] - h[i] - k)) {
cout << "NO
";
return;
} else {
m -= h[i + 1] - h[i] - k;
}
} else {
m += min(k - (h[i + 1] - h[i]), h[i]);
}
} else {
m += h[i] - h[i + 1];
m += min(k, h[i + 1]);
}
}
cout << "YES
";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
int T; cin >> T;
while (T--) run();
return 0;
}
C.Round Corridor
题意:
有一个圆盘,有两排,第一排等分成(n)块,第二排等分成(m)块。
现在给出两块,问这两块是否连通。
圆盘大概长这样:
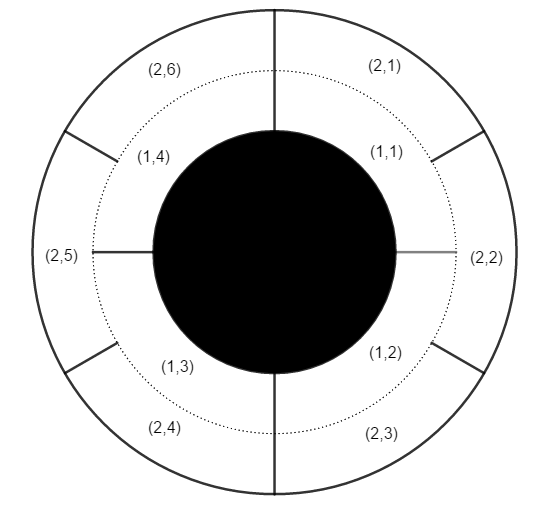
思路:
考虑两排的交界处,交界处会使得分割成若干个区域。
最终会分成(gcd(n, m))块区域,那么第一排每个区域的个数是(frac{n}{gcd(n, m)}),第二排每个区域的个数是(frac{m}{gcd(n, m)})
代码:
#include <bits/stdc++.h>
using namespace std;
#define debug(...) { printf("# "); printf(__VA_ARGS__); puts(""); }
#define ll long long
const int N = 1e5 + 10;
ll n, m; int q;
ll sx, sy, ex, ey, id1, id2;
ll gcd (ll a, ll b) {
return b ? gcd(b, a % b) : a;
}
void run() {
ll G = gcd(n, m);
n /= G; m /= G;
while (q--) {
cin >> sx >> sy >> ex >> ey;
id1 = (sy - 1) / (sx == 1 ? n : m);
id2 = (ey - 1) / (ex == 1 ? n : m);
cout << (id1 == id2 ? "YES" : "NO") << "
";
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
while (cin >> n >> m >> q) run();
return 0;
}
D.White Lines
题意:
给出一个(n cdot n)的矩形,里面有白点,有黑点。
可以选择一个(k cdot k)的矩形,将里面的点都染白,问如何选择是的白线的数量最多。
白线的定义为一行全是白的或者一列全是白的。
思路:
- 考虑先预处理出哪些行本身就是白线,哪些列本身就是白线。
- 然后考虑枚举矩形((l, r, up, down)),那么([1, l - 1])和([r + 1, n])的列的贡献和当前矩形无关,以及([1, up - 1])和([down + 1, n])的行的贡献和当前矩形无关
- 然后考虑矩形下移的过程,行的贡献可以预处理,因为矩形覆盖的([l, r])不会变,处理出哪些行的([l, r])之外的点都是白色的即可。
- 再考虑列的贡献,注意到对于一个列,黑点的最早出现位置为(Min), 最大出现位置为(Max),如果(Max - Min + 1 > k),那么这一列不会有贡献,否则当(down)移到(Max)的时候产生贡献,当(up)离开(Min)的时候失去贡献
代码:
#include <bits/stdc++.h>
using namespace std;
#define debug(...) { printf("# "); printf(__VA_ARGS__); puts(""); }
#define ll long long
const int N = 2e3 + 10;
int n, k;
char s[N][N];
int x[N], y[N], dx[N];
int Gx[N][N];
int add[N], del[N];
int get(int i, int l, int r) {
if (l > r) return 0;
return Gx[i][r] - Gx[i][l - 1];
}
void run() {
for (int i = 1; i <= n; ++i) {
cin >> (s[i] + 1);
}
x[0] = 0; y[0] = 0;
for (int i = 1; i <= n; ++i) {
bool F = 1;
for (int j = 1; j <= n; ++j) {
if (s[i][j] == 'B') {
F = 0;
break;
}
}
x[i] = x[i - 1] + F;
}
for (int j = 1; j <= n; ++j) {
bool F = 1;
for (int i = 1; i <= n; ++i) {
if (s[i][j] == 'B') {
F = 0;
break;
}
}
y[j] = y[j - 1] + F;
}
for (int i = 1; i <= n; ++i) {
Gx[i][0] = 0;
for (int j = 1; j <= n; ++j) {
Gx[i][j] = Gx[i][j - 1] + (s[i][j] == 'B');
}
}
memset(add, 0, sizeof add);
memset(del, 0, sizeof del);
int res = 0, dy = 0;
for (int j = 1; j <= k - 1; ++j) {
int Max = 0, Min = 1e9;
for (int i = 1; i <= n; ++i) {
if (s[i][j] == 'B') {
Max = max(Max, i);
Min = min(Min, i);
}
}
if (Max == 0) ++dy;
else if (Max - Min <= k) {
++add[max(1, Max - k + 1)];
++del[Min + 1];
}
}
for (int j = 1; j <= n - k + 1; ++j) {
dx[0] = 0;
for (int i = 1; i <= n; ++i) {
dx[i] = dx[i - 1];
if (get(i, 0, j - 1) + get(i, j + k, n) == 0) {
++dx[i];
}
}
int Max = 0, Min = 1e9;
for (int i = 1; i <= n; ++i) {
if (s[i][j + k - 1] == 'B') {
Max = max(Max, i);
Min = min(Min, i);
}
}
if (Max == 0) ++dy;
else if (Max - Min <= k) {
++add[max(1, Max - k + 1)];
++del[Min + 1];
}
int l = j, r = j + k - 1;
for (int i = 1; i <= n; ++i) {
int up = i, down = i + k - 1;
dy += add[i] - del[i];
res = max(res, y[l - 1] + y[n] - y[r] + x[up - 1] + x[n] - x[down] + dy + dx[down] - dx[up - 1]);
}
Max = 0, Min = 1e9;
for (int i = 1; i <= n; ++i) {
if (s[i][j] == 'B') {
Max = max(Max, i);
Min = min(Min, i);
}
}
if (Max == 0) --dy;
else if (Max - Min <= k) {
--add[max(1, Max - k + 1)];
--del[Min + 1];
}
}
cout << min(res, 2 * n) << "
";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
while (cin >> n >> k) run();
return 0;
}
E.Compress Words
题意:
给出(n)个字符串,要求接在一起。
后一个字符串可以选择一个最长的前缀去掉,但是要求这个前缀是前一个字符串的后缀。
思路:
前一个字符串最长只需要取后面那个字符串长度个后缀去和它做(Exkmp)即可。
代码:
#include <bits/stdc++.h>
using namespace std;
#define debug(...) { printf("# "); printf(__VA_ARGS__); puts(""); }
#define ll long long
const int N = 2e6 + 10;
char s[N], t[N], tt[N];
int n;
struct ExKMP {
int Next[N];
int extend[N];
//下标从1开始
void get_Next(char *s) {
int lens = strlen(s + 1), p = 1, pos;
//Next[1]要特殊考虑
Next[1] = lens;
while (p + 1 <= lens && s[p] == s[p + 1]) ++p;
//Next[2]初始化
Next[pos = 2] = p - 1;
for (int i = 3; i <= lens; ++i) {
int len = Next[i - pos + 1];
//第一种情况
if (len + i < p + 1) Next[i] = len;
//第二种情况
else {
//找到对于子串最靠后已经匹配的位置
int j = max(p - i + 1, 0);
//暴力匹配
while (i + j <= lens && s[j + 1] == s[i + j]) ++j;
p = i + (Next[pos = i] = j) - 1;
}
}
}
void work(char *s, char *t) {
get_Next(t);
int lens = strlen(s + 1), lent = strlen(t + 1), p = 1, pos;
while (p <= lent && s[p] == t[p]) ++p;
p = extend[pos = 1] = p - 1;
for (int i = 2; i <= lens; ++i) {
int len = Next[i - pos + 1];
if (len + i < p + 1) extend[i] = len;
else {
int j = max(p - i + 1, 0);
while (i + j <= lens && j <= lent && t[j + 1] == s[i + j]) ++j;
p = i + (extend[pos = i] = j) - 1;
}
}
}
}exkmp;
void run() {
int m = 0;
cin >> (s + 1); m = strlen(s + 1);
for (int i = 2; i <= n; ++i) {
cin >> (t + 1);
int lent = strlen(t + 1);
tt[0] = 0;
if (m < lent) {
for (int j = 1; j <= m; ++j) {
tt[j] = s[j];
}
tt[m + 1] = '�';
} else {
for (int j = m - lent + 1, i = 1; j <= m; ++j, ++i) {
tt[i] = s[j];
// cout << s[j] << " " << tt[j] << endl;
}
tt[lent + 1] = '�';
}
// cout << i << " " << (tt + 1) << endl;
exkmp.work(tt, t);
int Max = 0;
// cout << (tt + 1) << " " << (t + 1) << endl;
int lim = min(m, lent);
for (int j = 1; j <= lim; ++j) {
if (exkmp.extend[j] == lim - j + 1) {
Max = max(Max, exkmp.extend[j]);
}
// cout << j << " " << exkmp.extend[j] << endl;
}
for (int j = Max + 1; j <= lent; ++j) {
s[++m] = t[j];
}
s[m + 1] = '�';
// cout << (s + 1) << endl;
}
cout << (s + 1) << "
";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
while (cin >> n) run();
return 0;
}