LeetCode 1059. All Paths from Source Lead to Destination

原题链接在这里：https://leetcode.com/problems/all-paths-from-source-lead-to-destination/

题目：

Given the edges of a directed graph, and two nodes source and destination of this graph, determine whether or not all paths starting from source eventually end at destination, that is:

• At least one path exists from the source node to the destination node
• If a path exists from the source node to a node with no outgoing edges, then that node is equal to destination.
• The number of possible paths from source to destination is a finite number.

Return true if and only if all roads from source lead to destination.

Example 1:

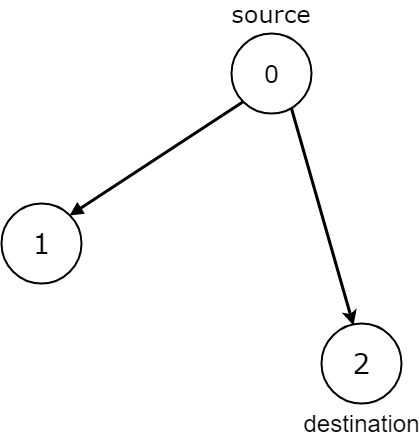
Input: n = 3, edges = [[0,1],[0,2]], source = 0, destination = 2
Output: false
Explanation: It is possible to reach and get stuck on both node 1 and node 2.

Example 2:

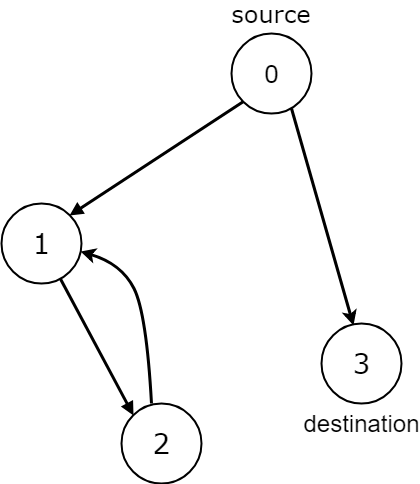
Input: n = 4, edges = [[0,1],[0,3],[1,2],[2,1]], source = 0, destination = 3
Output: false
Explanation: We have two possibilities: to end at node 3, or to loop over node 1 and node 2 indefinitely.

Example 3:

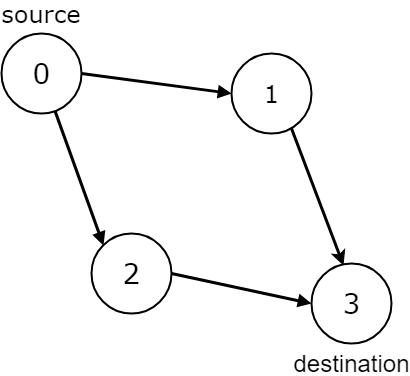
Input: n = 4, edges = [[0,1],[0,2],[1,3],[2,3]], source = 0, destination = 3
Output: true

Example 4:

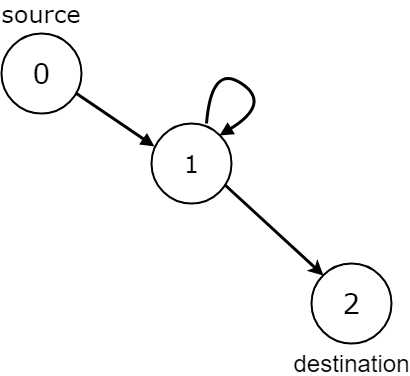
Input: n = 3, edges = [[0,1],[1,1],[1,2]], source = 0, destination = 2
Output: false
Explanation: All paths from the source node end at the destination node, but there are an infinite number of paths, such as 0-1-2, 0-1-1-2, 0-1-1-1-2, 0-1-1-1-1-2, and so on.

Example 5:

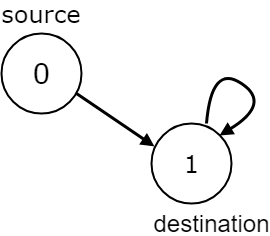
Input: n = 2, edges = [[0,1],[1,1]], source = 0, destination = 1
Output: false
Explanation: There is infinite self-loop at destination node.

Note:

1. The given graph may have self loops and parallel edges.
2. The number of nodes n in the graph is between 1 and 10000
3. The number of edges in the graph is between 0 and 10000
4. 0 <= edges.length <= 10000
5. edges[i].length == 2
6. 0 <= source <= n - 1
7. 0 <= destination <= n - 1

题解：

There are 2 cases it should return false.

case 1: it encounters a node that has no outgoing edges, but it is not destination.

case 2: it has cycle.

Otherwise, it returns true.

Could iterate graph with BFS. When indegree of a node becomes negative, then ther is cycle.

Time Complexity: O(n+e). e = edges.length.

Space: O(n+e).

AC Java:

class Solution {
    public boolean leadsToDestination(int n, int[][] edges, int source, int destination) {
        Set<Integer> [] graph = new Set[n];
        
        for(int i = 0; i<n; i++){
            graph[i] = new HashSet<Integer>();
        }
        
        int [] inDegrees = new int[n];
        for(int [] edge : edges){
            graph[edge[0]].add(edge[1]);
            inDegrees[edge[1]]++;
        }
        
        LinkedList<Integer> que = new LinkedList<Integer>();
        que.add(source);

        while(!que.isEmpty()){
            int cur = que.poll();
            if(graph[cur].size() == 0 && cur != destination){
                return false;
            }
            
            for(int nei : graph[cur]){
                if(inDegrees[nei] < 0){
                    return false;
                }
                
                inDegrees[nei]--;

                que.add(nei);
            }
        }
        
        return true;
    }
}

Could iterate by DFS too.

If current node has been visited within current DFS, then there is cycle.

When traversing all the nodes, make current node as done. 

Time Complexity: O(n+e).

Space: O(n+e).

AC Java:

class Solution {
    public boolean leadsToDestination(int n, int[][] edges, int source, int destination) {
        Set<Integer> [] graph = new Set[n];
        for(int i = 0; i<n; i++){
            graph[i] = new HashSet<Integer>();
        }
        
        for(int [] edge : edges){
            graph[edge[0]].add(edge[1]);
        }
        
        return dfs(source, destination, graph, new int[n]);
    }
    
    private boolean dfs(int cur, int destination, Set<Integer> [] graph, int [] visited){
        if(visited[cur] != 0){
            return visited[cur] == 2;
        }
        
        if(graph[cur].size() == 0){
            return cur == destination;
        }
        
        visited[cur] = 1;
        for(int nei : graph[cur]){
            if(!dfs(nei, destination, graph, visited)){
                return false;
            }
        }
        
        visited[cur] = 2;
        return true;
    }
}